One of the original blackjack side bets is the Insurance wager. This side bet pays 2-to-1 whenever the dealer’s hole card is a ten-valued card, otherwise it loses. This side bet is clearly countable by keeping track of the number of ten-valued cards relative to non-ten-valued cards. The only reason it has not been crushed by APs is because of two limitations on this wager. First, it can only be made when the dealer shows an Ace up, so that the player only has the opportunity to make this side bet once per 13 hands on average. Second, the Insurance wager size is limited to one-half of the player’s main blackjack wager. Without these two limitations, the “ten-in-the-hole” side bet would have long ago been abandoned.
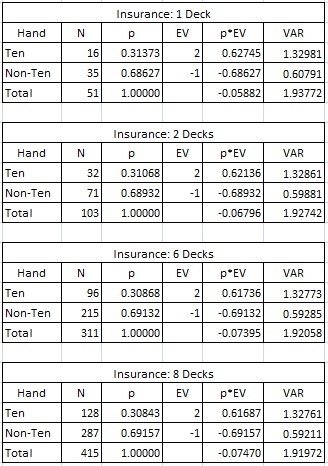
The house edge for Insurance is easy to compute. For example, in a single deck game, there are 16 face cards and 35 non-face cards (the Ace is already exposed). It follows that the true odds for Insurance are 35-to-16, while it pays 32-to-16. The edge on the Insurance bet is then 3/51, or 5.8824%. This is a fairly high house edge, hence the admonition to “never take Insurance.”
The following table gives the house edge and variance on Insurance for various numbers of decks:
Many gamblers and industry insiders alike don’t understand that Insurance is not part of the main game of blackjack. There is no rule that says this side bet must be offered. While almost no one makes this side bet, once per 13 hands the dealer has to ask the table for Insurance. If this takes 10 seconds (as the dealer waives her hand back and forth over the table), and the game is moving at 78 rounds per hour, then a full minute is consumed per hour with no benefit to the casino. That amounts to a loss of 1/60 = 1.67% of the total action at the table, and a corresponding incremental loss in revenue and decrease in hold. From a time and motion perspective, Insurance doesn't protect against disasters; Insurance is a disaster.
In addition to the time and motion issues Insurance has, the real estate lost to this side bet is tremendous. Typically, side bets are offered in a small circle next to the player’s main wagering area. However, Insurance usually appears on the layout like this:

Imagine the artwork or other wagering opportunities that could replace a banner that advertises a side bet that wastes time and is barely utilized. For example, the casino could advertise a restaurant or a show in this space.
To see that Insurance is susceptible to card counting, consider an AP playing single deck blackjack. On the first hand after the shuffle, suppose that the AP looks at his cards and those of one neighbor and sees only non-ten-valued cards. Then there are 31 non-ten-valued cards remaining in the deck, so that the odds of winning the Insurance bet are 31-to-16. Voila! The AP has an edge of 1/47 = 2.1277%.
From this example, it follows that there is a simple card counting system that performs perfectly in identifying when the Insurance bet is in the player’s favor. To describe it, we need a few variables. Let:
D = number of decks.
T = number of ten-valued cards that have been observed. Since there are 16 ten-valued cards per deck, it follows that the number of ten-valued cards remaining in the deck is 16*D – T.
N = number of non-ten-valued cards that have been observed. Since there are 36 non-ten-valued cards per deck, it follows that the number of non-ten-valued cards remaining in the deck is 36*D – N.
Then the odds of winning the Insurance bet are (36*D – N)-to-(16*D – T). The player has the edge over the Insurance wager whenever:
(36*D – N) / (16*D – T)
(36*D – N)
36*D – N
4*D
Next we look at card counting the Insurance bet. The Insurance count assigns the following tags to the cards: {+1, +1, +1, +1, +1, +1, +1, +1, +1, -2}. That is, every non-ten-valued card is assigned the tag +1, and every ten-valued card has the tag -2. The running count RC is kept as usual, by starting at RC = 0 with a fresh shoe, and adding the tag for each card played during the shoe. It follows that the running count after T ten-valued cards and N non-ten-valued cards have been played is:
RC = N – 2*T (Eq. 2)
Note that the right hands side of Eq. 2 is the same as the right hand side of Eq. 1. Combining Eq. 1 and Eq. 2, we see that the player has an edge whenever 4*D
Theorem The player has an edge over the Insurance side bet if and only if RC ≥ 4*D + 1
Therefore, using the Insurance count, the player should play the Insurance side bet at the following trigger running counts:
- For single-deck, RC equals 5 or higher.
- For double-deck, RC equals 9 or higher
- For six decks, RC equals 25 or higher.
- For eight decks, RC equals 33 or higher.
To compute the profitability from card counting the Insurance bet, I ran four simulations. These simulations were for 1-deck, 2-deck, 6-deck and 8-deck games. In single-deck blackjack, I assumed the player played head’s-up against the dealer and that five rounds were dealt between shuffles. For the multi-deck games I assumed a relatively deep placement for the cut card. The following table summarizes the results of my simulations:
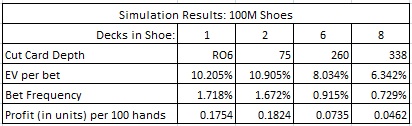
For example, in the two-deck game with the cut card placed at 75 cards, the AP will make an Insurance bet on 1.672% of his hands, and when he does, the AP's average edge will be 10.905% over the house. If the AP is wagering $50 on Insurance whenever he has the edge, and is getting 100 hands per hour, then the AP will earn $50 x 0.1824 = $9.12 per hour from the Insurance wager. However, the limitations on Insurance make it an opportunity which by itself has little value.
Let me give an example that underscores the true worth of Insurance for the basic strategy blackjack player. Suppose a basic strategy player is playing two-deck blackjack with the cut card placed at 75 cards. Suppose he is flat betting $100 on a high-roller game with good rules (S17, DOA, DAS) at a rate of 100 hands per hour. The baseline house edge on this game is 0.1928%. The basic strategy player will lose $100 x 100 x 0.1928% = $19.28 per hour on his blackjack play, but as shown above, will earn $9.12 from his Insurance play. Playing perfect Insurance reduces the player’s expected loss to $10.16 per hour, or in other terms, the house edge is now 0.1016%. In this game, perfect Insurance play reduces the house edge by over 47.3% of its original value.
Perfect Insurance play alone is not enough to give the AP an edge, but it can move the arrow strongly in that direction. More commonly, Insurance is used as a heuristic by management to help identify advantage players. Any player who makes the Insurance side bet when holding 8/5, while forgoing Insurance on his J/K will surely raise eyebrows.


