Side bets that pay out when the dealer busts were a hot area of development a few years back. I was involved with two of these bets as the primary mathematician for the game developers. One of the wagers I analyzed was Dealer Bust 21 (see this post). The other bust-type wager I analyzed was "Bet the Bust" (BTB) for the company Tech Art. BTB is the subject of this post.
Any time a wager pays on a dealer bust, there is a lot of excitement in the advantage player community that their beloved "hi-lo" betting system will identify situations when the dealer is more likely to bust. APs reason that an abundance of high cards will lead to more busted hands when the dealer is forced to draw. The error with this line of reasoning is that an abundance of high cards also leads to more pat two-card hands (totals of 17 or higher) negating the value of a high card as a "bust card." Nevertheless, BTB, more than any other "bust"-type side bet, has generated a lot of message board interest. The truth is, as usual, that hi-lo is not relevant to the discussion of card counting this wager.
I am personally a big fan of the Tech Art team, especially their owner Art Miller. Mr. Miller is best known for being the genius behind the ubiquitous peak devices that are installed in nearly every blackjack table in nearly every casino in the U.S. And, in all my years in the industry, he stands out as one of the nicest and most generous individuals I have had the pleasure to know. His attitude of "giving it away" is as rare as it is heartening.
THE RULES FOR PLAYING BTB
1. Wagers on BTB are placed after the dealer and all players have received their initial cards and the dealer has delivered his up card.
2. In the case that the dealer’s up card is either a Ten, Jack, Queen, King or Ace, the BTB wager is allowed after the dealer’s hand has been checked to see if it is a blackjack.
3. After viewing the up card of the dealer, if the dealer does not have blackjack, the player can choose to participate in the BTB bet.
4. If a player chooses to participate, an additional BTB wager is placed in the designated area on the layout.
5. The BTB side bet is resolved based on the final result of the dealer’s hand.
6. The player wins BTB if one or more players remain in the hand and the dealer busts his hand. The wager is then paid according to the designated pay table for the specified rules of the game and dealer up card.
7. The BTB wager is a push if no players remain in the hand to compete against the dealer after all players resolve their hands. In this case the dealer does not draw cards. Optionally, the dealer may always complete his hand if there is a BTB wager in action.
8. The player loses BTB if one or more players remain in the hand and the dealer makes his hand (achieves a total of 17, 18, 19, 20 or 21).
The following table gives the payouts based on the dealer up card and the rule for soft 17:
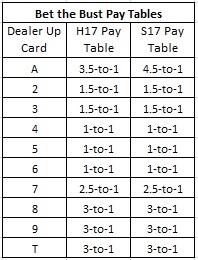
These two pay tables coincide except for the payout for a dealer Ace. The reason for the difference with an Ace is that in a H17 game, the dealer will bust more often when showing an Ace. This is because the dealer is forced to hit soft-17 hands, giving extra chances to bust that are not available on a S17 game.
There is a lot to the analysis of this bet. First, each of the different dealer up cards corresponds to a different wager with its own house edge and card counting system, and hence its own card counting vulnerability. Second, the house edge and card counting system may vary if the game is H17 or S17. Finally, the number of decks used (2, 6 or 8) will yield different edges and vulnerabilities.
It should come as little surprise that the greatest vulnerability turns out to be in the 2 Deck, S17 game. However, this game is very hard to find, whereas the 2 Deck, H17 game is quite common. Moreover, the 2D, H17 game is only slightly less vulnerable than 2D, S17. For these practical reasons, I am only going to present the analysis for the 2D, H17 game.
The following table gives the combinatorial analysis:
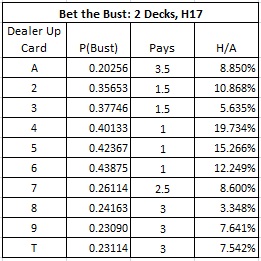
There is some question about how the edge is computed. To do this, I computed every way the dealer's hand could play out and simply counted how many of those corresponded to each outcome. These results are not computed by simulation; these numbers follow from a complete combinatorial calculation. This is not as difficult as it sounds, but I am going to omit the details.
To determine the vulnerability to card counting, I first computed the EOR's for each of these 10 wagers. Based on these EOR's, I came up with the following card counting systems:
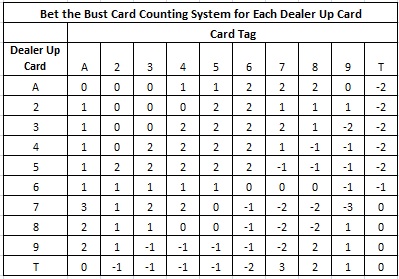
For example, to card count the "Bust on Dealer Ace" side bet (that pays 3.5-to-1), use the following card counting system (the top row in the table above):
A, 2, 3 = 0
4, 5 = +1
6, 7, 8 = +2
9 = 0
T,J,Q,K = -2
Note that this analysis illustrates that hi-lo is irrelevant to card counting this side bet for any dealer up card. None of the ten systems resembles hi-lo. In particular, in each system the Ace gets either a positive or neutral tag (the tag for an Ace in hi-lo is -1).
The following tables should crush the spirit of any would-be card counter of BTB:
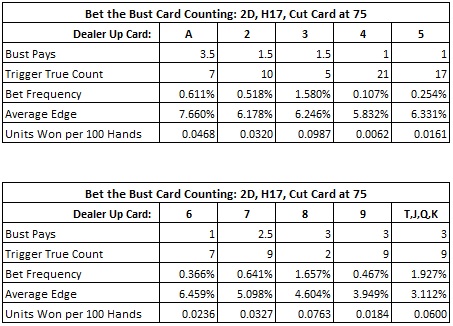
I note that the low frequencies for these side bets owes to two factors. To make the side bet, it must be the case that both the count is above the Trigger value AND that the given card is the dealer up card. It's this combination of factors that makes this wager such a challenge to count.
For example, the player who is dedicated to card counting the "Bust on Ace" side bet using the card counting system above will make a wager about 0.611% of the time (once every 164 hands). When he does make a wager, his edge will be, on average, about 7.660%. The "Bust on Ace" card counter will earn about 0.0468 units per 100 hands. With $100 wagers, that's under $5 per 100 hands. The most vulnerable side bet in this list is the "Bust on 3" side bet. This has a win-rate of about $9.87 per 100 hands with $100 wagers.
One could imagine (if one had a vivid imagination) a team of five card counters playing against the five most vulnerable bets on this list. A quick inspection shows that this team would count the following five wagers: bust on Ace, 3, 7, 8, T. Each card counter would count his individual wager. When the count got high enough to exceed his trigger, he would make the BTB wager on that up card. His team mates would follow suit, also making the BTB wager. In this way, each member of the team gets the full value as if he was counting all five of these wagers. Each of the five members of the team as a whole would then earn this entire amount.
The following table gives the statistics for a team approach to counting BTB:

For example, if the maximum bet is $25 on BTB, then this team (as a whole) will earn about $39 per 100 hands. In the grand scheme of advantage play, this win-rate puts BTB near the bottom, alongside delivering pizza for tips.
The possibility of card counting BTB reminds me of an old math joke:
Q. Why didn't the topologist study the empty set?
A. Because it's pointless.
Okay, maybe that went over your head. But let me just say, to a mathematician, that's pretty funny.


