Just after my book Advanced Advantage Play came out, a highly regarded AP asked me why I didn't include loss rebates against craps in it (I do cover exploiting loss rebates against baccarat, blackjack and roulette). He opined that I was no doubt saving it for myself. Today, casinos throughout Las Vegas and elsewhere in the U.S. offer loss rebates on craps to their top-tier players. Finding a craps game with 3-4-5x odds (or higher) with a loss rebate incentive of 10% (or higher) is like finding a pot of gold at the end of a rainbow -- it's magically delicious. But rainbows do exist and many APs are enjoying their pots of gold.
The profitability of playing against a loss rebate is a function of both the house edge and the standard deviation of the game. The higher the house edge, the lower the profitability for the AP. The higher the standard deviation, the more profit the AP can get from the game. A game with low house edge and high standard deviation is the ideal situation. Blackjack, with its microscopic house edge and high standard deviation is often the game of choice when it comes to beating loss rebates. As Don Johnson showed, a 20% loss rebate on blackjack can lead to profits in the millions of dollars.
As a reminder, to beat a loss rebate, a player comes into a game with two stopping points in mind, a win-quit point and a loss-quit point. If he hits his win-quit point, then he cashes out his winnings and leaves to come back another day with a fresh rebate in place. If he hits his loss-quit point, then he stops playing, collects his rebate, and leaves to come back another day with a fresh rebate in place. For a fixed game and loss rebate percentage, the questions to be answered are:
- What is the win-quit point?
- What is the loss-quit point?
- What is the player's expected win (in units) per session?
As you may recall from earlier times, I proved three theorems called the Loss Rebate Theorems that allow me to give a complete closed solution to the problem of finding these quit points and determining the profitability of the rebate.
For example, suppose a player is given a 20% loss rebate (Don Johnson), then the house edge is -0.2904% (6D, S17, DOA, DAS, LSR) and the standard deviation is 1.1417. Plugging this data into the Loss Rebate Theorem spread sheet gives:
- The player should quit after winning 24.11 units or after losing 25.97 units. His average expected win per session is then 1.25 units. His average session length is about 480 hands. With a $100,000 unit, his expected winnings are $125,000 per session.
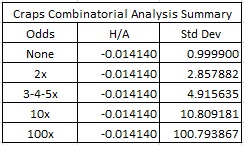
By comparison, consider a 20% loss rebate at craps with 3-4-5x odds. Assume the AP only plays pass line wagers and come bets, and always takes full odds. Then the house edge is 1.4140% and the standard deviation is 4.9156. Plugging this data into the Loss Rebate Theorem spread sheet gives:
- The person should quit after winning 91.79 units or after losing 98.87 units. His average expected win per session is 4.76 units. His average session length is about 376 pass/come decisions.
Do you see what I'm talking about now? In blackjack, under ideal circumstances with a 20% loss rebate, the AP earns about 1.25 units per session by exploiting his rebate. In craps with 3-4-5x odds, that number jumps to 4.76 units per session. That is, playing with a 20% loss rebate in craps is about 380% more profitable than the same rebate in blackjack. But it gets better. With 10x odds, the AP will win about 23.4 units per session with a 20% rebate. Holy crap(s)!
I now present the analysis for exploiting loss rebates in craps under the following circumstances:
- No odds, 2x odds, 3-4-5x odds, 10x odds and 100x odds.
- Loss rebates of 5%, 10%, 12%, 15%, 18% and 20%.
The following table summarizes the house edge and standard deviation for craps with the odds listed above:
The following tables give the details for each loss rebate amount and odds, as listed above;
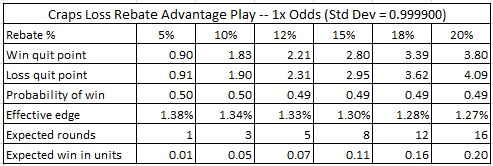
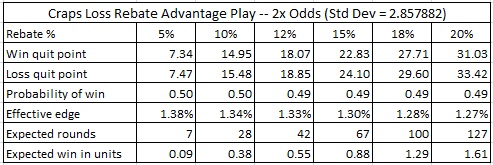
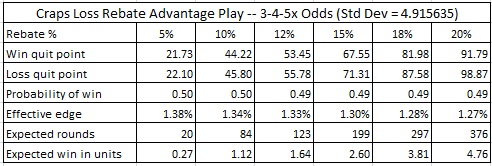
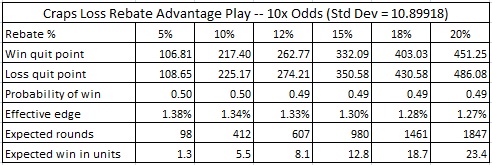
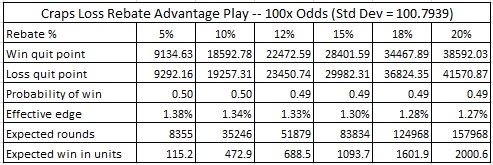
My opinion is that it is reasonable to offer a loss rebate in craps to high rollers, but that the conditions must be very carefully controlled. If you look through the tables above, consider only allowing those conditions that lead to less than one unit in potential profit per session. For players who only play pass line and come bet wagers, this means:
- With no odds, offer loss rebates up to 20%.
- With 2x odds, offer loss rebates up to 15%.
- With 3-4-5x odds, offer loss rebates up to 5%.
- With odds higher than 3-4-5x, DO NOT OFFER LOSS REBATES.


