In this blog post I explained edge sorting. For many years I have looked at the back of the playing cards Harrah's uses and wondered if it was feasible to edge sort those. Harrah's uses several different designs for their backs. Each of these designs is based on a geometric shape that is different from the "diamond" shape that is so easily sortable. Last week, I brought along a deck of Harrah's cards to the conferences, and during one of the less interesting talks I looked at them very closely. I admit to being a very distracted participant. At least I wasn't checking my text messages like several people seated near me. By the end of that talk I solved the design.
Here is the back of one of the cards from the deck I was studying:

By looking at the two vertical edges (left vs. right) or two horizontal edges (top vs. bottom) it would be very difficult to see the minor variations in real-time in order to create an effective sort. Such a defect would have to be observable and repeatable. There simply is no such defect. Similarly if you look at the stars that are along the edges of the casino-name boxes, there is no consistent defect to the pattern that would allow sorting. To see how precise the printing is, look at where the stars meet the upper box in the upper left corner and compare that to where the stars meet the lower box in the lower right corner. That's great printing!
If you like puzzles, then this card is a good one. I invite you to study it carefully before reading on.
The issue with this card can be seen by comparing the upper left corner with the lower right corner. Notice the shape of the three stars closest to this corner. In upper left, those three stars are bowed inward towards the center of the card. In the lower right, those three stars are bowed slightly outwards towards the corner of the card. Now suppose you rotate this card so that if it is a ten-valued card or Ace, then the card is turned so that this bow is oriented in one direction, and if it is a low card, then the card is turned so that bow is oriented in the other direction.
For a high card, you will see this: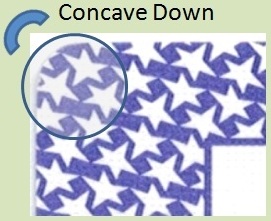
For a low card, you will see this: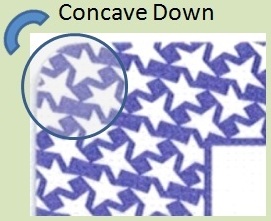
One way to understand this defect is to note that this concave up/down pattern exists on the back of the cards throughout the design. The outline of groups of six stars forms an oval shape tilted approximately 55 degrees on their major axis. It is simply a question of where along this oval shape that the corners are cut. Here is a picture of the embedded oval shape:
To test the viability of this method, I inspected every card in the deck. This defect was not clearly readable on all of the cards, but it was consistent enough that I felt it was worthy of an experiment. I sorted the deck as carefully as I could, knowing that in some cases I would not be able to read the card. I then tested my ability to read the cards several different times to conference attendees. I shuffled the cards (without a turn), cut them, and then by reading the backs, sorted about 30 cards from the deck into two piles (high vs. low). I completed this task as quickly as I could to try to model the speed that I would have to read the cards at the table. I then turned over the piles. In every case I missed a couple of cards. However, my accuracy rate was easily over 90%.
I highly doubt the minor defect I observed with these cards has ever been used in practice by APs. However, APs study everything about the game. They don't just look at the rules of the game, or consider card counting or hole-carding. They look at everything, especially possible defects with the equipment or procedure. Edge sorting is a powerful tool. Though the opportunities are rare, the edges obtained by APs can be very high while they use a method that is nearly impossible to detect. Know your cards!


