Mississippi Stud (MS) has more vulnerability to advantage play, by far, than any other proprietary table game or side bet. The scope of the game protection issues the game has stretches from collusion, to hole card play, to edge sorting, to others I don’t know about. The reason for all of these issues is the ability of the AP to place up to 9 extra units and then receive multiplied payouts when sufficient extra information is available. Because of these incidents, I began to consider the possibility of edge sorting MS (see this post to learn about edge sorting).
After a bit of experimentation with the help of Bill Zender, I decided to explore the very simple sort into two groups, Jacks vs. everything else:
- Group 1 = Jacks.
- Group 2 = non-Jacks.
The reason for choosing Jacks instead of Queens, Kings or Aces, is that Jacks are involved in the greatest number of straights.
A review of the way MS proceeds is important to a complete understanding of the way edge sorting works for the game. First, the player is dealt 2 cards, denoted P_1 and P_2. Then three cards are placed face down in front of him. These three cards will be exposed in order as the Flop (F), Turn (T) and River (R) cards.
The letter “J” will refer to a Jack. For the player’s first card, I will use the letter “A” when it is not a Jack. The player’s second card will be referred to by the letter “B” when it is not a Jack. Then there are four possible player starting hands:
AB, JB, AJ, JJ.
Next, consider the three edge-sorted dealer cards, Flop, Turn, River, that are face-down in front of the AP. I will use the letter “X” for a non-Jack on the Flop, “Y” for a non-Jack on the Turn, and “Z” for a non-Jack on the River. There are then eight different edge-sorted groups of cards the AP can distinguish:
XYZ, JYZ, XJZ, XYJ, JJZ, JYJ, XJJ, JJJ.
There are then 4x8 – 1 = 31 possible combinations for the distribution of Jacks between the player’s hand and the three face-down cards (the combination player = JJ, board = JJJ is impossible). The following table gives the combinatorial analysis for edge sorting MS. This computation shows a player edge of 38.489% for the AP who is edge sorting MS with the Jack, non-Jack sort.
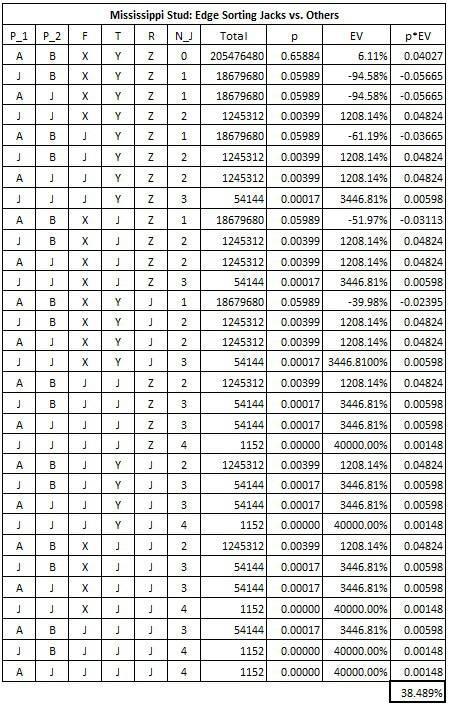
The AP edge of 38.489% for observing three sorted cards in MS is significantly higher than observing three edge sorted cards in Three Card Poker (16.076% edge) or five edge sorted cards in Caribbean Stud (6.899% edge).
The first question that arises is to determine perfect strategy for the AP. I only solved this question for the Flop wager, after the AP views his two cards and the edge sorts of the three hidden cards. The following eight Excel files give details for each player hand for each of the eight dealer edge-sorting groupings. The first two columns give the player’s cards. The third column gives the EV of folding on the Flop. The fourth column gives the EV of raising 1 unit on the Flop. The fifth column gives the EV of raising 3 units on the Flop. The final column gives the basic strategy decision.
This is way too much information. To simplify this, I considered the 169 distinct starting player hands. For the dealer groups JJZ, JYJ, XJJ, JJJ, it is clear that the AP is going to raise 3 units throughout the hand, regardless of his starting cards. So the only real decision point for the AP is what to do against the dealer hands XYZ, JYZ, XJZ and XYJ.
The following pdf file contains the basic strategy for the Flop betting decision:
Mississippi_Stud_Two_Card_Edge_Sort_Strategy
In my opinion, the full strategy for edge sorting MS is well beyond the capability of all but, perhaps, the most exceptionally brilliant APs. However, the full strategy isn’t necessary. Playing perfect two-card strategy and using common sense for the Turn and River decisions should be more than sufficient to crush MS.
In an effort to better understand the power of edge sorting MS, I decided to investigate a subset of these hands to quantify the gain the AP gets. In discussing strategy for MS, it is convenient to group the cards into three categories:
- Low Cards (L) = {2, 3, 4, 5}
- Mid Cards (M) = {6, 7, 8, 9, T}
- High Cards (H) = {J, Q, K, A}
Basic strategy says to fold any two non-paired Low cards. It is also correct to fold all Low card, Mid card starting hands (except for the hand 5, 6 suited). Clearly, if the AP knows that there are either two or three buried Jacks in the dealer’s down-cards, then he is going to go all-in (bet 3 units throughout the hand). This change in strategy results in a gain that can be precisely quantified. The following table summarizes this gain:
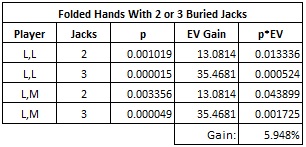
From this table, we see that the AP gains 5.948% over basic strategy with these hands alone. That is, the AP already has a 1.033% edge over the house by just making the basic strategy changes (fold => all-in) indicated in this small subset of hands.
Another way to get a sense for the EV gain and change in strategy is to examine some specific hands. The following tables gives EV details for the Flop decision for four different player starting hands:
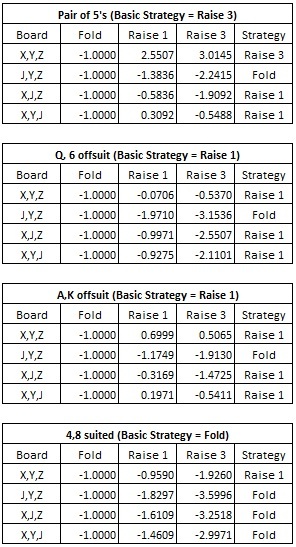
In my opinion, edge sorting MS must be considered to be the most extreme case of vulnerability to edge sorting of any casino table game, proprietary or otherwise.
The following are my suggestions for protecting MS from an edge sorting vulnerability:
- Tactical decision point: Make sure there is a turn included in every shuffle procedure, even when the game is being dealt from an automatic shuffler.
- Strategic decision point: Use safe cards.


