I recently received the following question from a reader:
I asked at Wizard of Vegas (WOV) in this thread to analyze the probabilities for Four Card Poker's (FCP) Bad Beat Bonus (BBB) wager. The game boasts a house edge of 20.3% but WOV's analysis came to 19.5%. They felt it was due to Shuffle Master computing the odds by evaluating each hand as if it came from a separate deck. By that I assume they mean that if the dealer has Quad Kings, there is no way the player could have the same hand. Does this mean that all of Shuffle Master’s games are calculated this way and that all their "bonus wagers" are actually offering a house edge that is slightly lower than what is advertised?
I recently completed the analysis of advantage play for FCP; it is given in this blog post. In that post I noted the inaccuracy in the computation done by Shuffle Master and Elliot Frome. My simulation, which supports the computation given by James Grosjean, gives a house edge for FCP of approximately 2.9%. Stanley Ko gives an edge of about 3.40% using a simple strategy. A simulation I completed supported Ko’s result. Shuffle Master gives the edge as 1.58% in this document. Elliot Frome claims to have a strategy to return 1.50% in this document.
Because of this discrepancy, the question above was interesting to me. One source of advantage play opportunities are mathematical errors. A game that goes into a casino with bad math can lose a lot of money. For the main game of FCP, the apparent error favors the house in the case of the main game: the house edge is higher than the advertised edge.
This game was not easy to analyze. I had to complete several significant initial steps before I could write the final code.
- I had to re-write evaluation functions for four-card poker hands.
- I had to create a hash function that evaluated all four-card poker hands and assigned a positive integer to that hand. These integers were between 1 and 7013, and gave the hand’s absolute rank among all four-card hands. I exported this data to a file.
- For the main program, I read the data file into an array of size allHands[52][52][52][52] that allowed the hand rank to be instantly looked up rather than re-computed in the main program.
- Last, and most important, was to cycle over “equivalence classes” of five-card poker hands rather than all poker hands. The equivalence is over all suit-permutations. For example, the hand (4C, 5D, 5H, 6S, 7C) is equivalent to (4D, 5H, 5S, 6C, 7D). There are 134459 equivalence classes, which is far less than the full cycle of five-card poker hands (2598960 of them).
With this in mind, let’s return to the questions at hand. The BBB is a side bet for FCP that wins if either the player or dealer has a hand that is two-pair or better and is beaten by the other hand. Here is the pay table for this wager:
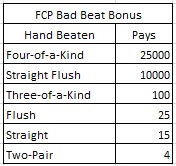
In this document Shuffle Master claims the following statistics for this wager:
- House edge = 20.3%
- Hit frequency = 5.6%
The first question the poster makes is if Shuffle Master’s results are correct. The poster states that an edge of 19.5% is the consensus at WOV. As it is given there, the house edge that poster JB computed through a full combinatorial analysis is 19.4722%.
A full cycle consists of 134459 x combin(47,6) = 1,443,763,328,007 hands (about 1.4 trillion hands). It took 4.5 hours to run the cycle. The following table gives the full combinatorial analysis of BBB:
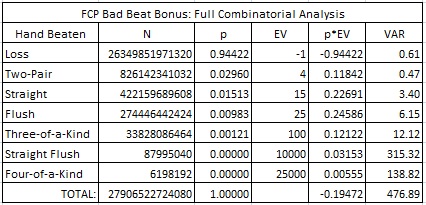
In particular, note that this combinatorial analysis gives:
- House edge = 19.47%
- Hit frequency = 5.58%
- Standard deviation = 21.84
My result is exactly the same as the house edge claimed in the WOV thread of 19.4722%. The hit frequency matches that given by Shuffle Master.
The second question the poster makes is if it is possible that Shuffle Master computed the house edge for the BBB wager by assuming that the player hands and dealer hands were dealt from separate decks. The following table gives the full combinatorial analysis for the BBB assuming the player and dealer are dealt cards from separate decks:
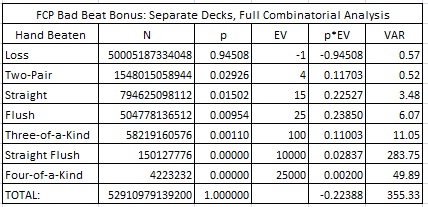
This combinatorial analysis gives the following statistics:
- House edge = 22.39%
- Hit frequency = 5.49%
- Standard deviation = 18.85
Both the house edge and hit frequency obtained through this method are significantly different from those stated by Shuffle Master. I conclude that Shuffle Master did not make the assumption of separate decks in its computation.
The game of Four Card Poker is a significant mathematical and programming project. It is clear that errors have been made, and those errors appear to be on the side of Shuffle Master. In the case of the BBB, the error favors the player. That is, the house edge is less than claimed in the documentation submitted by Shuffle Master.
That such errors exist should give pause to any individual in casino management. What if the error favored the player to the extent that there was no longer a house edge at all? What if the player had an edge off-the-top? It might sound like this is uncommon. It happens all the time. Some of the biggest fortunes APs have made resulted from faulty game mathematics.
To avoid a potential disaster based on faulty mathematics:
- If your casino is the first to put in a new table game, offer it only at a low table maximum until significant data from live play has been collected.
- If your casino is putting in an established game, independently verify its performance. Do this by either contacting another casino with the game or by conducting an independent analysis.
- No matter who, everyone can make a mistake.


