One of the most common blackjack side bets in California card rooms is known as Buster Blackjack (BBJ). I found this documentation online. The player who makes the BBJ wager wins if the dealer busts. The payout is then based on the total number of cards in the dealer’s busted hand. There are a lot of details to share, so I’ve decided to break up the discussion into the six-deck case and the two-deck case. This article covers card counting BBJ in a six-deck shoe game.
When I was asked about the vulnerability of BBJ to card counting by one of California’s largest banking corporations, I told them “not very.” After all, the dealer needs low cards to generate hands with lots of cards, he needs mid-cards to give stiff totals of 15 and 16, and he needs high cards to bust hands. My intuition was both right and wrong: the difference is the pay table. There are eight different pay tables for BBJ that are in use or recommended. I investigated all eight and found that five of these eight are vulnerable and three are not. There is also a progressive version of BBJ that I did not investigate at all.
To begin with, I am going to focus on one specific vulnerable pay table for BBJ. This is the most common pay table used by card rooms banked by one of the largest corporations in California. The pay table is as follows:
- Dealer busts with 8+ cards pays 200-to-1.
- Dealer busts with 7 cards pays 100-to-1.
- Dealer busts with 6 cards pays 30-to-1.
- Dealer busts with 5 cards pays 6-to-1.
- Dealer busts with 4 cards pays 3-to-1.
- Dealer busts with 3 cards pays 1-to-1.
- Otherwise, the player loses the BBJ bet.
Here is the combinatorial analysis for this pay table:
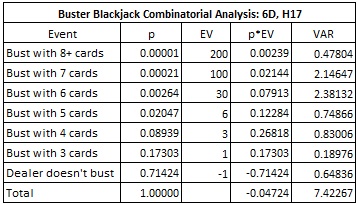
In particular,
- The house edge is 4.724%.
- The standard deviation is 2.724.
- The hit frequency is 28.576%.
The following table gives the effect of removal (EOR) for each card. The EOR tells the change in house edge by removing a single card of that rank and re-computing the house edge. A positive EOR means that the edge moves towards the player side if the card is removed. A negative EOR means that the edge moves towards the house side if the card is removed.
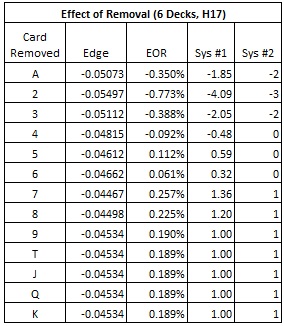
Notice how much larger the EOR is for the cards A, 2, 3 than for any other card. With an abundance of these three cards in the shoe, the dealer is more likely to have hands with a large number of cards. Whether the dealer’s hand busts or not is beside the point to beat this pay table: the primary goal is to have multi-card hands. Removing a single deuce from a six-deck shoe moves the edge towards the house by 0.77%. That’s big. Also, an Ace never busts with fewer than four cards. Removing an Ace from the six-deck shoe moves the edge towards the house by 0.35%.
In the table above, under the column Sys #1, I give tags for the optimal card counting system #1. I simply use the EOR’s to two decimal places, scaled to make the index for a ten-valued card equal to 1. System #1 is not intended to be used in practice. I include it only for purpose of determining an upper bound for the profit possible by card counting BBJ.
Under the column Sys #2, I give a balanced card counting system that can be used in practice. System #2 shows the importance of the cards A, 2, 3 to the card counter, with deuces the most valuable card. The betting correlation for this system is 0.977. For math geeks, this value is the cosine of the angle between the vectors given by system #1 and system #2. The closer this value is to 1, the more accurate the system.
To analyze these two systems, I simulated one hundred million (100,000,000) six-deck shoes, with the cut card placed at 260 cards (1 deck from the end), for each system. The following table summarizes the results of these simulations:
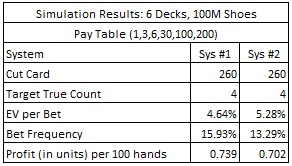
Note that system #2 returns 95.0% of the profit that optimal system #1 returns.
These numbers indicate a moderate vulnerability to advantage play. If the AP uses system #2 against BBJ on a fast heads-up game where he gets 200 rounds per hour, and the AP makes a $100 wager on BBJ whenever he has the edge, then the AP can earn $140 per hour on the BBJ side bet. The AP using system #2 will have an average edge over the house of 5.28% and will make the BBJ bet on 13.29% of his hands.
As I mentioned at the start of this post, there are eight different pay tables that I considered for BBJ. The following table gives the combinatorial analysis for another pay table in common use:
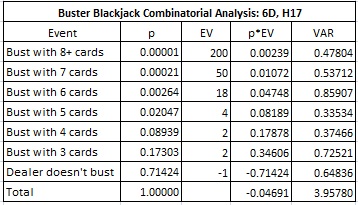
In particular
- The house edge is 4.691%.
- The standard deviation is 1.989.
- The hit frequency is 28.576%.
Because a hand that contains an Ace does not bust with fewer than four cards, the increase in payout for busting with three cards does not come into play with a hand that includes an Ace. Moreover, busting with four or more cards has greatly reduced payouts. These two factors eliminate the effectiveness of Aces to the card counter.
The following table gives the EOR’s for this pay table, along with a card counting system based on these EOR’s. In particular, notice how much the EOR for the Ace has changed.
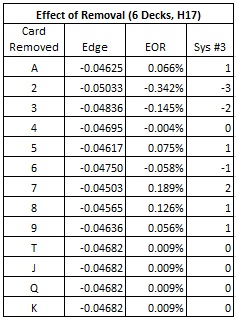
System #3 is a reasonable choice, based on the EOR’s. The betting correlation for this system is 0.973.
I was very surprised at how different the tags for this pay table are from those developed for the previous pay table. This highlights the profound difference in strategy involved in beating these two pay tables. I know of no other blackjack side bet that has as significant a strategy change for the AP based purely on the pay table being used.
To analyze this pay table and system #3, I ran a simulation of twenty million (20,000,000) six-deck shoes, with the cut card placed at 260 cards. The results were very disappointing for the AP:
- The trigger count is +8.
- The average edge is 2.33%.
- The bet frequency is 3.64%.
- The number of units won per 100 hands is 0.085.
These numbers indicate a very low vulnerability to advantage play. If the AP uses system #3 on a fast heads-up game where he gets 200 rounds per hour, and the AP makes a $100 wager on BBJ whenever he has the edge, then the AP can earn about $17 per hour.
There are two other pay tables that are similar to this one, paying 2, 2, 4 units respectively for busting with 3, 4 or 5 cards. Simulations against these other pay tables showed an even lower vulnerability to card counting. Because of their low vulnerabilities, I will not include these pay tables in any further discussion of card counting BBJ.
The following table summarizes the combinatorial analysis for six different pay tables for BBJ:
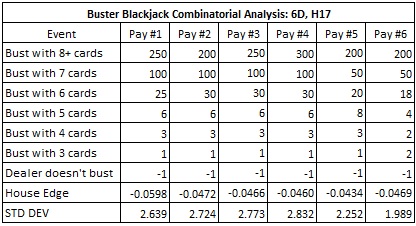
The following table gives the results of card counting BBJ against each of these six pay tables.
- For pay tables #1, #2, #3, #4 and #5, I used system #2 with tags (-2, -3, -2, 0, 0, 0, 1, 1, 1, 1).
- For pay table #6, I used system #3 with tags (1, -3, -2, 0, 1, -1, 2, 1, 1, 0).
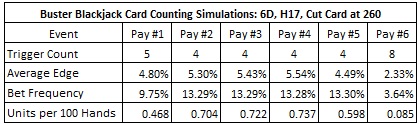
The only difference between pay tables #2, #3 and #4 is the top award. For pay table #4, the AP can earn about 0.737 units per 100 hands by card counting BBJ. This is as good as it gets for the AP using system #2 in a six-deck shoe game.
The relative weakness of card counting using system #2 against pay table #5 surprised me; I thought it would do better. These results may be because system #2 was designed for pay table #2. A different count may work better against pay table #5. I’ll leave the development and evaluation of that card counting system as an exercise to the reader.
Normally, at this point, I would simulate various penetration levels in the shoe to demonstrate the effectiveness of cut-card placement on game protection. I would then make recommendations for protecting BBJ that follow a standard game protection model for card counting blackjack side bets. In this case, however, it is completely clear how to protect BBJ.
I have only one game protection recommendation for BBJ, and it’s easy:
- In a six-deck shoe game, only offer versions of BBJ with a pay table that pays 2-to-1 when the dealer busts with 3 or 4 cards.


