Of all the currently available side bets for blackjack, the news that Lucky Ladies (LL) is vulnerable to card counting has been out the longest. The reason is simple: LL pays for any player total of 20, so ten-valued cards are a premium. This is exactly the same situation the counter wants for the main game of blackjack. The bulk of the effort of early APs was to quantify the profit attainable by using one of the standard card counting systems against LL, like the High-Low system. This effort was misguided. Few APs understood then, and few understand now, that LL is uniquely vulnerable to a specialized count.
What most APs missed during these glory days was that if they are playing against the LL bet then they should not be counting cards at blackjack. There was plenty of profit available from LL alone. Instead, most APs who lived in their “blackjack card counting”-centered universe brought attention to themselves by their bet spread and play variation. The correct strategy was to play break-even blackjack, track the specialized LL count, and when the trigger count was exceeded, make a maximum bet on LL. This simple tactical approach was both safe and highly profitable.
In 2003, I shared the specialized count I developed with an AP based in Washington State. Within a year he told me that he earned over $100k playing against LL. However, his situation was unique. He found several double-deck games dealt to between 80 and 90 cards, with a maximum bet of $100 on LL. Under the ideal playing conditions he found, his expected profit was over $300 per hour.
These extreme instances of a highly profitable LL game are now very rare. Nowadays, nearly all casinos that offer LL have a maximum bet of $25 and are fully aware of this card counting vulnerability. Casinos watch LL the same way they watch ordinary blackjack. The tells of the LL counter are the same as the blackjack card counter. Players who are card counting LL are easy to spot and are routinely backed off.
There are different pay tables for the LL bet for a double-deck game and a six-deck shoe. Here is the combinatorial analysis for each, where QH = “Queen of Hearts.” I also include the analysis when the double-deck pay table is used for the six-deck shoe game. In particular, note the high variance of this game in all versions. The QH pair contributes over 4% to the total return.
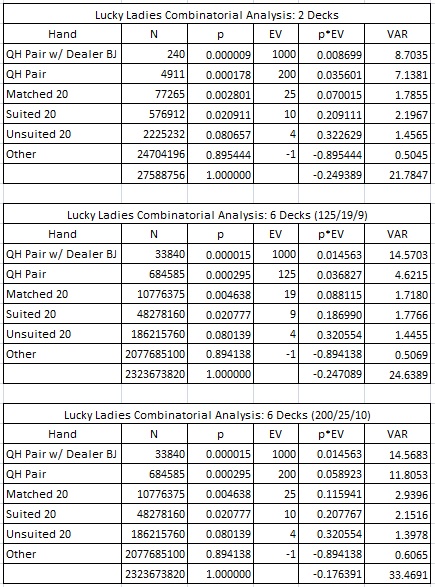
It is not necessary to give details for the effect of removal or determine the theoretically best indices to the fraction of a percent. It’s clear that the player wants to have ten-valued cards and does not want low cards (2 to 8). The borderline cards are the A and 9 that can form the rare hand A-9 with a total of 20. And, obviously, the QH is extremely valuable. I will first consider the double-deck game.
To get a baseline performance for a blackjack card counting system, I simulated using the High-Low system (-1,1,1,1,1,1,0,0,0,-1,-1,-1,-1) against the LL bet. I assumed a double-deck game where the cut card was placed at 75 cards (29 cards from the end). For convenience, I will refer to two decks of cards as a “shoe.” Here are the results from a simulation of one hundred million (100,000,000) shoes of LL using the High-Low system, with the cut card placed at 75 cards.
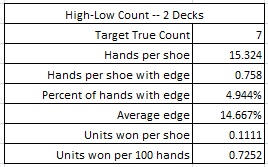
If the maximum bet is $25, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the High-Low count will earn about $36.26 per hour from LL.
A more reasonable count is a simple “Ten count.” In this count, each of the cards 2, 3, 4, 5, 6, 7, 8, 9 is given the tag +1 and the cards T, J, Q, K are given the tag -2. This balanced count is obviously stronger than the High-Low count. However, a small modification will add a bit more oomph to it. Simply give the first QH the tag -4 and the second QH the tag 0. This maintains the balance of the count, while adding focus to a key card.
Here are the results from a simulation of one hundred million (100,000,000) shoes of LL using this modified Ten count, with the cut card placed at 75 cards:
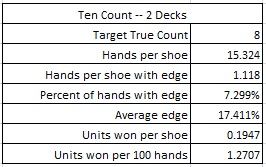
If the maximum bet is $25, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the modified Ten count (first QH = -4, second QH = 0) will earn about $63.54 per hour from LL. This count gives 75.2% more return than the High-Low count.
It is important for game protection to understand the extreme sensitivity of LL to deck penetration. One of the most successful ways to protect LL is to deal fewer cards per shoe. The following table makes this clear
Next, I present the Optimal LL count I developed for the double-deck game in 2003. The point is to give full value to the QH payouts and the 20’s that arise from two ten-valued cards. To do this, the aces are given the tag +1. In order to balance the count, the first QH is given the value -10 and the second QH is given the value -2. The justification for the first QH being given the value -10 is that once the first one is dealt, the QH pair is impossible.
Here are the results from a simulation of one hundred million (100,000,000) shoes of LL using the Optimal LL count, with the cut card placed at 75 cards:
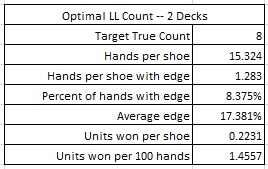
The AP has an edge on about 8.38% of the hands he plays and the average edge he has when he makes the LL bet is over 17.3%. If the maximum bet is $25, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the Optimal LL count (first QH = -10, second QH = -2) will earn about $72.79 per hour from LL. This count gives 100.7% more return than the High-Low count and 14.5% more return than the modified Ten count.
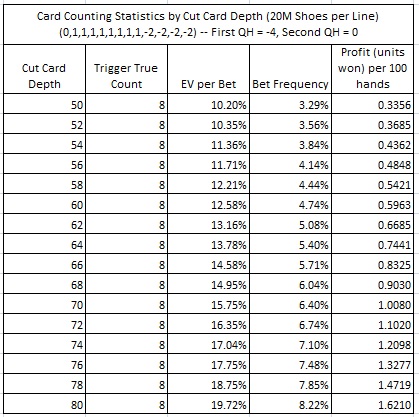
The following table gives the return of the Optimal LL count by cut card depth:
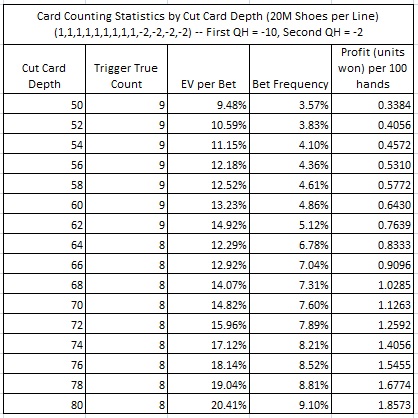
The Optimal LL count was the count uses by the AP mentioned above in Washington State. To understand his earning potential, he was playing a game with the cut card placed a depth of more than 80 cards. He was earning at least 1.857 units per 100 hands. Playing heads-up, getting 200 rounds per hour, with a maximum bet of $100, his expected return was over $370 per hour. No wonder he was so happy.
This AP sent a picture I want to share. Even though I work on the other side of the tables as a consultant, I respect APs right to do what they do for a living, and I am not about to give away a (former) friend's identity. For that reason, I have edited out the smiling face of the AP from this photo:

The vulnerability of LL in the six-deck version is far less than the double-deck case. Because of the high variance and low return, it is unlikely that the AP will target this version. Because there are six QH in the shoe, the effect of removing one of them is not as high as the double-deck case. For that reason, I only considered the ordinary Ten count (0,1,1,1,1,1,1,1,1,-2,-2,-2,-2).
Here are the results from a simulation of one hundred million (100,000,000) six-deck shoes of LL using the Ten count, with the cut card placed at 260 cards. This simulation is for the 1000/125/19/9/4 pay table
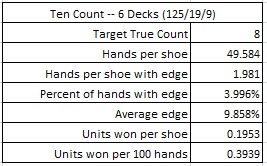
If the maximum bet is $25, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the Ten count on a six-deck shoe game will earn about $19.70 per hour from LL. This is significantly less earning potential than using the weakest system (High-Low) against the double-deck version.
Here is a simulation of one hundred million (100,000,000) six-deck shoes of LL using the Ten count, with the cut card placed at 260 cards. This simulation is for the situation when the 1000/200/25/10/4 pay table (the one that's usually used for two decks) is used on the six-deck game:
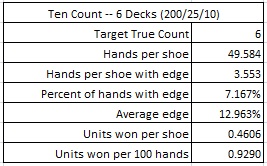
If the maximum bet is $25, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the Ten count on a six-deck shoe game with the 200/25/10 pay table will earn about $46.45 per hour from LL. This is a strong edge for the AP, about the same as placing the cut card at 67 cards in a double-deck game. For this reason, the double-deck pay table should be used with caution on a six-deck shoe game.
The next table considers a simulation of one hundred million (100,000,000) eight-deck shoes of LL using the High-Low count, with the cut card placed at 338 cards (1.5 decks from the end). This simulation is for the situation when the 1000/200/25/10/4 pay table (the one that's usually used for two decks) is used on the eight-deck game:
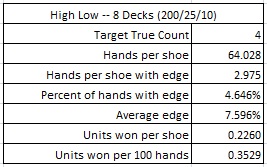
If the maximum bet is $25, and the AP is playing heads-up, getting 200 rounds per hour, then the AP using the High-Low count on an eight-deck shoe game with the 200/25/10 pay table will earn about $17.65 per hour from LL. This is a weak edge for the AP. The High-Low count is ineffective as a dedicated LL count.
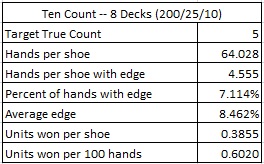
The next table considers a simulation of one hundred million (100,000,000) eight-deck shoes of LL using the Ten count, with the cut card placed at 338 cards (1.5 decks from the end). This simulation is for the situation when the 1000/200/25/10/4 pay table (the one that's usually used for two decks) is used on the eight-deck game:
Here is the combinatorial analysis for this version:

The baseline house edge for this version (eight-decks with double-deck pay table) of LL is only 16.7326%. I strongly advise casinos not to offer this version of LL.
I have heard some rumors that LL has also been attacked in the six-deck version by shuffle tracking. This seems reasonable to me. Any slug of face cards that is trackable will give the AP a strong opportunity.
Safeguarding LL is quite trivial, but it is important to understand that it is extremely vulnerable if it is not protected. The following are my recommendations for protecting LL:
- Watch for players who usually play LL late in the deck at a maximum bet. These players may spread to multiple hands when they play LL.
- In a six-deck shoe game, watch for players who play a maximum LL bet for a certain number of hands per shoe and otherwise don’t play the bet.
- Decreasing penetration has a strong effect in neutralizing AP opportunities.
- Do NOT use the double-deck pay table on a six-deck game.
- Watch for the other tells of an ordinary card counter.


