Match the Dealer (MD) is a popular side bet offered with six-deck Spanish 21. I have never seen this wager offered on ordinary blackjack, though it is certainly possible. The wager is similar to the Pair Square side bet, paying for pairs with a premium for suited pairs. In the Pair Square bet, the player wins based on the ranks and suits of his two initial cards. In MD, the player wins if either of his two initial cards has the same rank as the dealer’s up-card. There are two other side bets that are based on the player’s initial two cards and dealer up-card: 21 + 3 and Lucky Lucky.
Spanish 21 is almost universally offered as a six-deck shoe game using "Spanish" decks. Here is the combinatorial analysis of the MD side bet: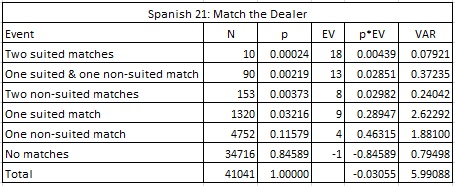
In particular:
- The house edge is 3.055%
- The hit frequency is 15.411%
- The standard deviation is 2.448
This article considers card counting MD.
First, recall that Spanish 21 is a variant of ordinary blackjack that uses “Spanish” decks. These are ordinary decks with the Tens removed, leaving 48 cards per deck. In a Spanish shoe, there are six Spanish decks, for a total of 288 cards, instead of the normal 312 cards per shoe. It follows that pairs are more likely in a Spanish shoe: instead of a frequency of 1-in-13.52 for a pair in a normal six-deck shoe, in a Spanish shoe, pairs occur with frequency 1-in-12.48.
The way to view beating a bet like this is that a significant imbalance in either the rank or suits of the remaining cards in the shoe favors the player. For example, consider a Spanish shoe with 144 cards remaining (half a shoe). If there are 12 of each card remaining, then the total number of rank-pairs is 792. However, if the frequencies are {10, 10, 10, 10, 10, 10, 14, 14, 14, 14, 14, 14} (10 cards each for 2, 3, 4, 5, 6, 7 and 14 cards for each of 8, 9, J, Q, K, A) then the total number of rank-pairs is 816. A similar computation shows that any imbalance in suits yields more suit-pairs. Given that the goal is to keep track of rank or suit imbalances, I considered three card counting systems.
The first count I considered is the “Rank count.” In this count, I grouped the cards into two subsets of six cards each. One group consisted of the low cards {2, 3, 4, 5, 6, 7}, which are given the tag +1. The other group consisted of the high cards {8, 9, J, Q, K, A}, which are given the tag -1. If the true count is sufficiently positive, then a pair of high cards is more likely. If the true count is sufficiently negative, then a pair of low cards is more likely. For this reason, the “target true count” refers to a value that indicates both a positive and a negative target.
I simulated one hundred million (100,000,000) six-deck Spanish shoes using the Rank count. The cut-card was placed at 240 cards (48 from the end). The following table summarizes the result from this simulation:
An AP using the rank count should make the MD wager whenever the count is either 10 or higher or -10 or lower. Then the AP will make the MD wager on about 1.28% of his hands, and when he does make the wager, his average edge will be about 2.06%. An AP who finds a game that allows a maximum wager of $100 on MD and is able to play heads-up, getting 200 rounds per hour, will earn about $5.28 per hour playing against MD.
The next count I considered is called the “Frequency count.” Rather than grouping the cards into two sets, this metric keeps track of the exact number of cards remaining from the most played rank and least played rank. Subtract the min from the max of these values to get a “running count.” Then convert that running count to a true count. If the true count is sufficiently large then the AP will have the edge.
For example, mid-way through the shoe, if the distribution of ranks is (11, 10, 9, 8, 7, 6, 13, 14, 15, 16, 17, 18), then the max is 18, the min is 6, the running count is max – min = 18-6 = 12, and the true count is 12/3 = 4.
This method is not human-feasible, but it is still worth checking its performance. The following table summarizes the results from a simulation of one hundred million (100,000,000) six-deck Spanish shoes using the Frequency count: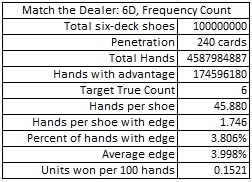
An AP using the Frequency count should make the MD wager whenever the true count is 6 or higher. Then the AP will make the MD wager on about 3.81% of his hands, and when he does make the wager, his average edge will be about 4.00%. An AP who finds a game that allows a maximum wager of $100 on MD and is able to play heads-up, getting 200 rounds per hour, will earn about $30.42 per hour playing against MD. If this count was human-feasible, it would represent a significant improvement over the Rank count and would indicate a vulnerability. However, it is highly unlikely that any AP (or team of APs) could use this count in practice.
Finally, I considered the “Suit count.” This count is similar to the Frequency count, except this count keeps track of the exact number of cards remaining from the most played suit and least played suit. Subtract the min from the max of these two values to get a “running count.” Then convert that running count to a true count. If the true count is sufficiently large, then the AP will have the edge.
For example, mid-way through the shoe, if the distribution of suits is (24, 32, 40, 48), then the max is 48, the min is 24, the running count is max – min = 48 – 24 = 24, and the true count is 24/3 = 8.
To test this count, I conducted a simulation of one hundred million (100,000,000) six-deck Spanish shoes using the Suit count. I discovered that this count is not sufficient to gain a meaningful edge. The following table summarizes the results of this simulation: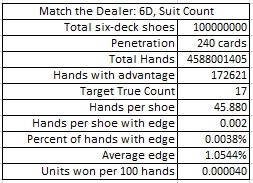
A cursory comparison of the Suit count with the much easier Rank count shows that the Suit count is essentially worthless. It is both more complicated to use than the Rank count and returns significantly fewer units per 100 hands.
It is well-known that the base game of Spanish 21 has a significant card counting vulnerability. Outside of blackjack, it is the only variant that has a book describing how to use card counting against it. However, in my opinion the MD side bet is a very weak opportunity for APs. Honestly, I can't imagine that APs will ever target MD through card counting. (Underscore "card counting.")
No casino defense is indicated.


