(flim′flam′) noun 1. nonsense; rubbish; humbug (ref. Webster's New World Dictionary)
I am never bothered by popular gambling flimflam. Those who believe in timing, progression or pattern systems live in a world where elephants appear in clouds and tea leaves predict their love lives. The gaming industry thrives on illusory pattern perception, which appears to be part of the genetic framework of our species. And baccarat is foremost among the games where players believe that mysterious patterns allow them to predict future events.
By contrast, advantage players are seeking a gaming-world without illusion. They look beyond patterns and fortune-telling. Most APs are intellectually curious and deserve fact-based analysis, not flimflam. False AP information also harms casinos. While APs may be losing their bankrolls, casinos may be expending their limited resources chasing dead ends. Flimflam can be hard to distinguish from the real thing. In the end, everyone is harmed.
In this post I gave an absolute upper bound on the possible winnings from baccarat using computer-perfect play. I showed that a player who makes a $1000 wager on the Banker or Player bet whenever he had the edge, and made no other bets, would earn at most $1.58 per shoe. Any card counting system would earn less. As I showed in this post, the practical profit per shoe using a card counting system is about 15 cents.
In search of AP baccarat card counting flimflam, I did a Google search on “baccarat card counting.” Here are the first 5 entries: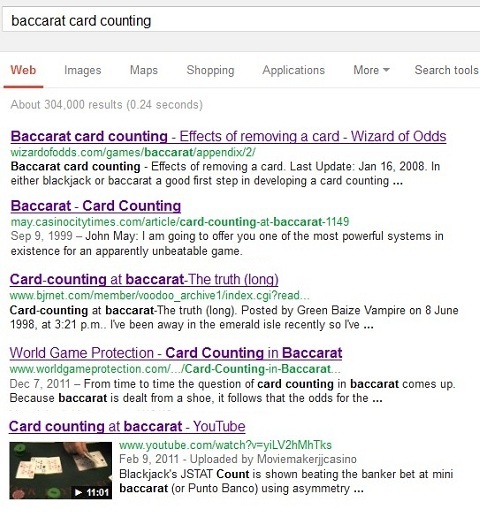
The first entry is at the Wizard of Odds website, where Michael Shackleford concludes: “I hope this section shows that for all practical purposes baccarat is not a countable game.” I cannot seriously imagine using the word "flimflam" in the same sentence with the name "Michael Shackleford."
The second entry is by well-known baccarat author John May, who commonly goes by the monikers “GBV” and “Green Baize Vampire” on Internet message boards. May wrote a book about baccarat, “Baccarat for the Clueless,” where he covers more sophisticated methods, including shuffle tracking, card warps and dealer errors.
Certainly, the lead sentence of this article is a gross exaggeration: "... I am going to offer you one of the most powerful systems in existence for an apparently unbeatable game." Later in the article, May stated:
“Griffin summed up his analysis by stating that a card-counter could earn no more than seven cents per day by using the strongest possible count system. While the greater part of what these highly respected theorists say is true, it is not impossible to create a card-counting system which can win to a greater extent on the tie bet.”
May’s article is actually devoted to beating the “Tie” bet, not the main game. His analysis is imperfect and he exaggerates its value, but it is not false and it is certainly not flimflam.
The third entry is another article by John May on the topic of card counting the Tie bet in baccarat. This is a post on a message board forum. In it, May again understands the truth that the Banker/Player bets in baccarat cannot be card counted, as he points towards the Tie bet when he says:
“It seemed to me that regardless of Griffin's conclusion, it might be possible to design a winning system for baccarat. This is because attempts to design workable baccarat systems had largely concentrated on bank/player, which is a waste of time.”
The fourth entry is an article I wrote that was posted on the World Game Protection web site (this website has since been taken down). In it, I concluded:
“From card marking, to card location techniques, to false shuffles, to shuffle tracking, to outright cheating, there are fortunes that are made over the baccarat tables. But these fortunes are not being made by card counting.”
This leaves only the fifth and final entry on the Google list, the YouTube video "Card Counting at Baccarat" by John Stathis, who goes by the Internet moniker “JSTAT.” Before you read any further, I encourage you to watch the first minute of this video.
In this minute, you hear Stathis state:
- “To win at baccarat we need a true count of +8.”
- “Here is a demonstration; I took out sixteen 2-thru-9s each, plus the Aces.”
- “Tens are -2, non-tens are +1, Aces equal 0, bet Banker at true count +8.”
Stathis gives a specific card counting system and a specific target true count above which he claims the player will have the edge if he bets on Banker.
To double-check these claims, I searched for his system and found a message board post by Stathis that read, in part:
“Buy 8 decks of cards and remove 16 A-9 each to prove the effectiveness of this count by playing it at home. This gives us an initial running count of +128, more than enough to give us a small advantage betting on the banker … Divide the running JSTAT Count (10,J,Q,K = -2, 2,3,4,5,6,7,8,9 = +1, aces = 0) with the number decks remaining to get the true count. We need a true count of at least +8 to nail the casinos with banker bets … Don't expect to win more than 1% of your total banker bet advantage action.”
In this quote, Stathis appears to be saying that the AP will be able to get an edge over the house. To get this edge, he advises using the balanced Ten count with tags {0,1,1,1,1,1,1,1,1,-2} (note. Stathis calls this the “JSTAT count”). Stathis advises making a wager on the Banker bet at a true count of +8 or higher.
To analyze Stathis’ claims, I began by completing a simple combinatorial analysis. In the video, Stathis sets up a demonstration with a shoe that has sixteen 2-thru-9s removed. In the order {A, 2, 3, … , 9, T} this leaves the following distribution in the shoe: {32, 16, 16, 16, 16, 16, 16, 16, 16, 128}. It was not clear from what Stathis said if he also removed sixteen Aces, in which case the shoe distribution would be {16, 16, 16, 16, 16, 16, 16, 16, 16, 128}. For that reason, I ran the combinatorial analysis of each. Here is the combinatorial analysis of the shoe {32, 16, 16, 16, 16, 16, 16, 16, 16, 128}: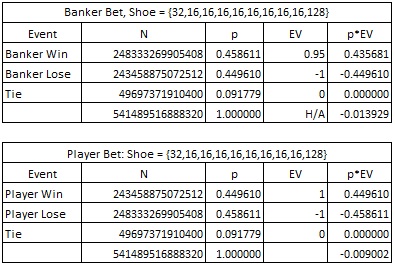
Here is the combinatorial analysis of the shoe {16, 16, 16, 16, 16, 16, 16, 16, 16, 128}: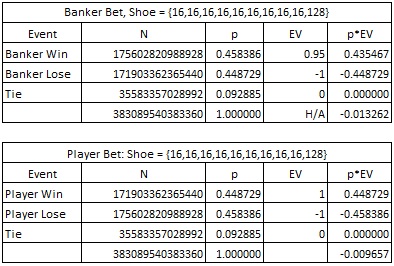
Stathis appears to claim that the player has the edge making Banker bets. In fact, the house has the edge (1.3929% and 1.3262%, respectively), and that edge is higher than the off-the-top Banker-bet edge of 1.0579%.
Stathis advises making Banker bets when the true count is +8 or above. In the first combinatorial example above, the true count is +23.1. In the second combinatorial analysis, the true count is +24.5. From these examples, it appears that the Ten count is negatively correlated with a Banker edge.
Subsequent to the publication of this post, Stathis added the following comment at the start of his video (which may have been modified by the time you read this):
In this disclaimer, Stathis requests a computation. In the standard game, with no cards removed, the Banker bet wins 45.8597% of the hands. The scenario referred to in the disclaimer is covered by the second combinatorial analysis given above. In that analysis, the Banker bet wins 45.8386% of the hands. Therefore, the claim that the Banker bet will win more often is false.
In an attempt to assess the full value to the AP, I ran a simulation of card counting Baccarat using the Ten count. I simulated one-hundred million (100,000,000) eight-deck shoes, with the cut-card placed 14 cards from the end of the shoe.
As can readily be seen, the Ten count is negatively correlated to the Banker bet. The higher the Ten count, the higher the edge for the house. In particular, if the AP makes a wager on the Banker bet whenever the true count is +8 or higher, then:
- The AP will make a Banker wager on 5.912% of the hands.
- The average house edge when the AP makes a Banker wager is 1.199%.
- The AP will lose, on average, 0.0506 units per shoe.
- The AP will lose, on average, 0.0622 units per 100 hands.
An AP who wagers $1000 on the Banker side whenever the true count is +8 or higher will lose, on average, about $62.20 per 100 hands. Here is Stathis' response, posted on 01/16/2013:
Here is a twitter post made by Stathis on 01/17/2013:
The high-ranking of Stathis' video in a Google search indicates that this information may be frequently accessed in decision-making considerations by both APs and casinos. The existence and promotion of these claims is potentially harmful to both APs and casinos.
APs may be harmed because they may believe they are using a winning system when the system has been demonstrated to lose. Those APs who are not well grounded in the mathematics of advantage play and rely on experts may not be able to distinguish factually incorrect advice. Professionals do not need faulty tools.
Likewise, casinos may be harmed because they may be drawn again into the false belief that baccarat is susceptible to card counting. There are far too many serious threats to baccarat to pull game protection down blind alleys. Casinos certainly don't need pointless paranoia.
Articles, books, videos and posts on card counting baccarat (and card counting other games) are noticed by both sides of the table, and therefore intellectual honesty is paramount.


