The baccarat Tie bet allows the player to wager that the result of the next hand of baccarat will be a tie between the Player and Banker hands. This wager is a standard part of the layout, like insurance in blackjack. The desire to card count the main game of baccarat dates back to Dr. Ed Thorp of “Beat the Dealer” fame, who wrote “… no practical winning strategy is possible for the Nevada game, even with a computing machine playing a perfect game.” I addressed card counting baccarat in this post and this post. From what I can tell, no serious attempt has been made to study computer-perfect play or card counting against the Tie bet. This post corrects this deficit in the literature.
There are two common pay tables for the Tie bet, one paying 8-to-1 and the other paying 9-to-1. Surprisingly, casinos have found that the Tie bet is played more often with the 8-to-1 payoff, because many Asians believe that “8” is a lucky number. The following tables give the combinatorial analysis for the Tie bet:
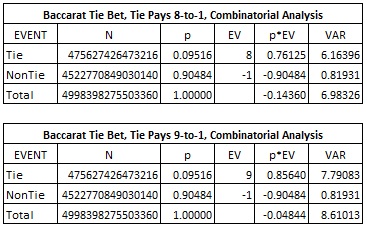
In particular, the 8-to-1 version has house edge 14.360% and the 9-to-1 version has house edge 4.844%.
The Te bet was scrutinized for advantage play by author John May, who wrote about his findings in his book: “Baccarat for the Clueless." His method involves an end-play. If the remainder of the shoe is rich in even cards (cards with values 0, 2, 4, 6, 8), then because the sum of two even numbers is an even number, hands will be more likely to result in an even-number tie. In this magazine article, he claims the player can earn 0.00504 units per shoe, with a bet frequency of 0.01% (once per 10,000 hands) and an average edge of 62%. I am not going to double-check his work, but no serious AP would go after an opportunity with those numbers.
I am going to first consider the 8-to-1 version. To get a sense for its potential, I conducted a simulation of 100,000 shoes. For each shoe, I computed the house/player edge at the exact point in the shoe when there were 26 unseen cards. I then plotted the results:
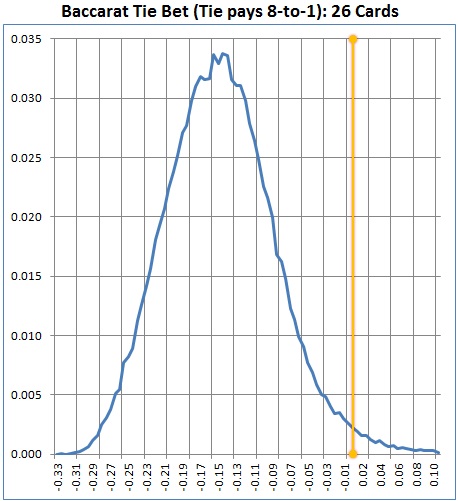
The horizontal axis gives the house/player edge. The vertical axis gives the probability that the edge occurs. The part of the distribution to the right of the orange vertical line corresponds to the profit potential for the AP. The frequency of the player having the edge is simply the area under the curve to the right of the vertical line. The average edge is the weighted mean (balance point) of the portion under the curve to the right of the vertical line.
To be more specific, with 26 unseen cards:
- The player will have the edge on 1.89% of the shoes.
- The player’s average edge (when he has the edge) is 4.62%.
However, these numbers do not mean the 8-to-1 cannot be beaten in the right circumstances. A player commented that he found an online game where the last round may be dealt with 7 unseen cards. In this situation, the player can easily use a computer program to determine when to take the Tie bet.
With 7 unseen cards:
- The player will have the edge on 31.41% of the shoes.
- The player’s average edge (when he has the edge) is 35.17%.
Here is the distribution:
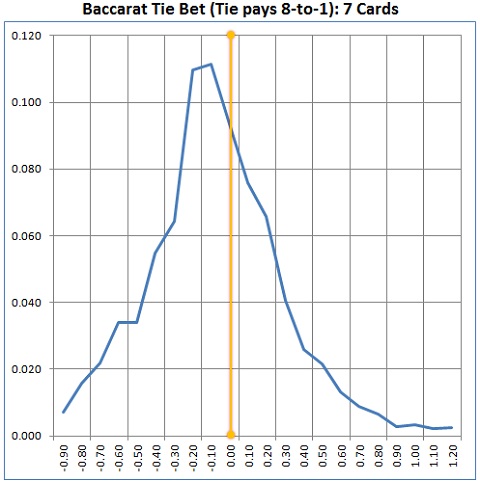
A simple linear approximation gives an upper bound of about 0.33 units per shoe using computer-perfect play when the 8-to-1 game is dealt down to 7 unseen cards.
These numbers are consistent with John May’s findings. In a brick-and-mortar game with the cut card placed at 14 cards, there is almost nothing there in the 8-to-1 game. The AP is going after such a small part of the distribution, while using imperfect tools, that the wager is essentially unbeatable.
The same cannot be said for the 9-to-1 version. In this case there is definitely a sizable portion of the distribution to the right of the orange vertical line. By conducting simulations at various points towards the end of the shoe, I estimated the potential earnings from computer-perfect play. The following slide show plots the distributions of the edges for the 9-to-1 version of the tie bet, for various numbers of unseen cards from 18 to 66. Each slide was obtained by a simulation of 100,000 shoes.
The average edge and bet frequency for each distribution is given in the following table:
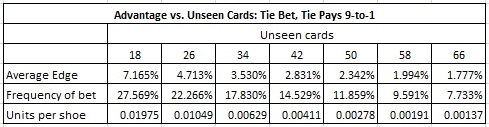
I used this data to get an absolute upper bound on the potential earnings from advantage play against the 9-to-1 Tie bet. Because a hand uses at least 4 cards, an upper bound is obtained by summing the values in the row “units per shoe” and multiplying that value by 2. It follows that:
Tie bet earnings per shoe ≤ 0.094 units.
This allows us to fully quantify the vulnerability of the Tie bet. If a person is allowed to use a computer program to tell them when to play the Tie bet, and that person makes a $100 wager on the Tie bet whenever they have the edge, then the player will earn at most $9.40 per shoe.
The next step is to see if there is a practical (legal) way to get a piece of that $9.40 per shoe profit. To do this, I developed a card counting system to use against the tie bet. The first step was to consider the effect-of-removal (EOR) for each card. The EOR simply gives the change in the house edge obtained by removing each card from the shoe and re-computing the house edge. The final column simply multiplies each value in the EOR column by 3,300. This was done to help generate a reasonable card counting system.
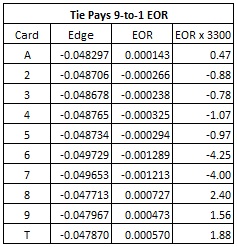
By looking at the final column, I investigated the card counting system with tags:
- A = 0
- 2, 3, 4, 5 = -1
- 6, 7 = -4
- 8, 9, T = 2
This card counting system appears to be new to the lexicon of baccarat. It is also non-intuitive. In an attempt to get a feeling for why this should be the right card counting system, I considered when a tie was likely to occur. It occurred to me that the edge for the tie bet would change based on the number of cards required by the hand. Here are those edges:
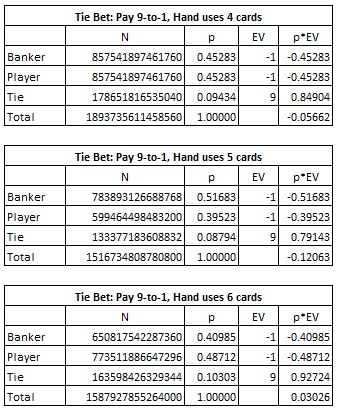
From these computations, we see that the player has an edge of 3.026% on the Tie bet if he knows in advance that the hand will require six cards. How does the card counting system with tags (0, -1, -1, -1, -1, -4, -4, 2, 2, 2) fit with this observation?
It is clear that the cards 8 and 9 are those that are least likely to result in a hand requiring six cards; hence the edge moves towards the player side as those cards are removed. Meanwhile, the cards 6 and 7, when dealt as the fifth card, almost always require that a sixth card also be drawn. Hence these cards favor the house as they are removed from the shoe. Shoes rich in 6s and 7s and poor in 8s and 9s lead to a significant increase in hands requiring six cards.
I ran a simulation of one-hundred million (100,000,000) shoes of baccarat, using the card counting system above with tags (0, -1, -1, -1, -1, -4, -4, 2, 2, 2). The cut card was placed at 14 cards, as usual. This simulation was for the 9-to-1 pay table. The following table gives statistical information from this simulation:
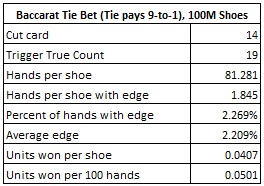
This simulation shows that the AP should make the Tie bet whenever the true count is +19 or above. If he does, then he will make a Tie bet on 2.269% of his hands, with an average edge of 2.209% whenever he makes the Tie bet. If the AP wagers $100 on the Tie bet whenever the count hits the trigger count, then the AP will earn about $4.07 per shoe.
The earnings computed above, $4.07 per shoe, represents 43.3% of the maximum $9.40 per shoe earnings available from computer-perfect play. The card counting approach is not particularly efficient, but it is far superior to the end-play method suggested by John May.
Perhaps the greatest barrier to advantage play against the Tie bet is the lack of availability of the 9-to-1 payoff. I surveyed a number of land-based casinos and could not find it available anywhere. Players would rather wager on the higher house edge but “lucky” 8-to-1 payoff. However, the 9-to-1 payoff is frequently found in live-play online baccarat, giving a unique opportunity for the AP and for the player using computer-perfect play.
The safest protection from the casino-side is to simply continue offering the 8-to-1 pay table. If your casino offers the 9-to-1 pay table, watch for players who make large Tie bets towards the end of the shoe. There isn't much there, but that doesn't mean they won't go for it.


