(flim′flam′) noun 1. nonsense; rubbish; humbug (ref. Webster’s New World Dictionary)
Flimflam arises in many different areas of scientific investigation, but one unifying feature is its deleterious effect on those who need fact-based information to properly do their jobs. Though I understand that gambling flimflam is a necessary part of the industry from the player's side, it is critically important that those on the casino side have access to a qualified rebuttal. In particular, the notion that baccarat, or the baccarat Tie bet, can be effectively card counted drives unnecessary and costly paranoia inside the casino industry. Rather than paying attention to substantial game protection issues, valuable resources are expended chasing ghosts.
In this post, I presented the case against John Stathis’ (a.k.a. JSTAT) claim that the balanced Ten count with tags (0,1,1,1,1,1,1,1,1,-2) can be used to card count ordinary baccarat. As part of that post, I presented the following image showing the top five Google results based on the search “baccarat card counting.”
The second and third entries are made by the well-known baccarat author John May, who commonly goes by the monikers “GBV” and “Green Baize Vampire” on Internet message boards. May wrote the book, “Baccarat for the Clueless,” which has been one of the top-selling books on baccarat over the last decade. While the facts about card counting baccarat that May presents are roughly correct, he has certainly created unfounded concern for casino management. When management sees that there are books that present factually winning baccarat systems, some have a hard time distinguishing big from little, danger from drivel. A book about baccarat card counting must mean that there are armies of card counters beating the game. This is a false conclusion that demands a rebuttal.
Because of the fallout when I published my card counting system for the EZ Baccarat Dragon side bet in October of 2011, I have been hardened against the danger of overreaction. Casino management must understand when a system that wins in theory is, at best, a novelty item in the modern AP’s arsenal. One function of this blog is to give a comparative analysis of an array of advantage play opportunities so that such an overreaction does not occur again. This is done by obtaining three numbers for a candidate game: the average edge the AP has when he makes the bet, bet frequency, and the AP's win per 100 hands. What follows is my comparative analysis of May's system.
The heart of May’s system can be found in his article, “Card-counting at Baccarat” that appeared in the September, 1999 issue of Casino City Times:
“… it is not impossible to create a card-counting system which can win to a greater extent on the tie bet … For example, say there are no odd cards remaining in the pack. There are only 5 possible totals: 0,2,4,6,8. The odds of a tie are doubled. You have an advantage of 62% on average … You can detect such a situation by assigning a value of +1 to odd cards. When (and if) your count reaches 160, you know that the average distribution of cards will give you a huge 62% advantage.”
In other words, May is recommending the unbalanced card counting system, where:
- odds (1,3,5,7,9)= +1
- evens (0,2,4,6,8) = 0
- Target running count = +160.
To understand the number 160, note that there are exactly 5x32 = 160 odd cards in an eight-deck shoe, therefore all the odd cards have been depleted from the shoe at a running count of +160. A running count of 160 leaves only even cards in the shoe.
May states that the advantage for the player is 62%, on average, in this situation. To verify this, I completed the combinatorial analysis for the Tie bet, assuming a fresh shoe with all the odd cards removed from it. The following table presents the combinatorial analysis in the case the Tie bet pays 8-to-1: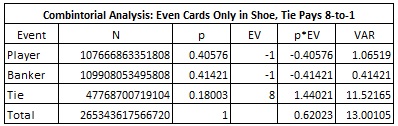
We see that the player edge is 62.023% in this situation, validating May’s claim. That’s a big edge, no doubt, so the issue all comes down to bet frequency. May does a kitchen-table computation in his article to get an estimate for the bet frequency of his system:
Assuming we make our last wager having seen all but a generous 8-13 cards we can calculate the opportunity by the following methods: The chance of 8 even cards appearing on the bottom of the deck is mathematically the same as 8 cards off the top. This is given by dividing 416 by 256 (total number of even cards) to determine the chance of one even card appearing, then multiplying this figure by the result of 415 divided by 255, and so on until we reach 404/244. Then take the probabilities of having this extreme subset occur for 8 through to 13 cards, add them up, then divide by 6. It turns out we will encounter an all-even subset roughly once in every 10,000 hands!
The gist of May’s claim is that if the game is being dealt so that the final round occurs with between 8 and 13 cards remaining, then the bet frequency for his system is about 1-in-10000 hands. To explore May’s claim about the bet frequency, I ran simulations of his card counting system with cut-card placements of 12, 14, 16, 18, and 20 cards. I assumed the standard baccarat cut-card rules:
- If the first card is the cut card, then two more rounds are dealt before the shuffle.
- If the cut card comes out mid-round, then one more round is dealt before the shuffle.
A cut-card placement shallower than 12 cards may result in insufficient cards to complete the last round. The standard cut-card placement using the "ribbon spread" is at 14 cards. May's work is based on the last round being dealt with 8, 9, 10, 11, 12 or 13 cards remaining. It follows that May was assuming the last round was dealt according to the standard cut-card rules, with a cut-card placement at the traditional location of 14 cards. In my simulations, I assumed the counter could see the initial burn cards (not usually the case), so these cards were included in the running count.
The following table summarizes the results of my simulations when the Tie bet pays 8-to-1: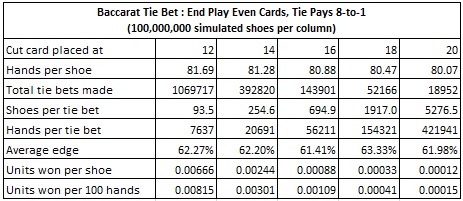
With the cut card placed at the standard position of 14 cards, the frequency of making a Tie bet using May’s system is once per 20691 hands. The error in May’s computation above is his assumption that each of the situations of having 8, 9, 10, 11, 12 and 13 cards are equally likely.
The indicated bet frequency of one wager per 20691 hands is equivalent to one Tie bet per 254.6 shoes. At a pace of 1.25 hours per shoe, May’s system yields one Tie bet wager per 318.3 hours of play. A player who watches a baccarat table for 8 hours per day will make a Tie bet using May’s system, on average, once every 39.8 days.
With a cut-card placement at 14 cards, if the AP places $1000 on the Tie bet whenever he has the edge, and at no other time, then the AP will earn, on average, $3.01 per 100 hands over the long run. The AP will earn $8.15 per 100 hands with the cut card placed at 12 cards.
It would be quite a sight for casino management to observe a player sitting patiently at a baccarat table 8 hours per day for over a month, then suddenly place a $1000 wager on the Tie bet. Yet, this appears to be what May's is recommending for the AP. His equivocation is similar to someone winning the lottery reconciling their win into an hourly wage.
In his article in the Casino City Times, May states:
“So, given initial bankroll of $50,000 you ought to bet roughly $3800. You would expect to win an amazing $2,356 on average each time you made this bet … This represents an earning per hundred hands of roughly $24 …”
With a cut card placement at 14 cards, my simulations show a win rate of $11.44 per 100 hands, with a $3800 wager. With a cut card placement at 12 cards, my simulations show a win rate of $30.97 based on a $3800 wager. As above, I believe May’s error has to do with his assumption about the equal distribution of hands with 8, 9, 10, 11, 12 and 13 cards remaining.
For the record, here is the combinatorial analysis in the rare situation when the Tie bet pays 9-to-1: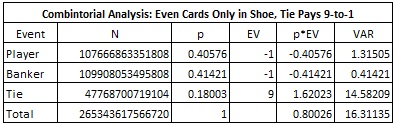
Here are the results of my simulation of May’s card counting system when the Tie bet pays 9-to-1: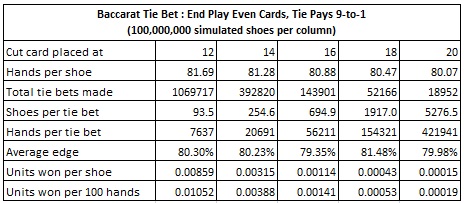
With a cut-card placement at 14 cards, if the AP places $1000 on the Tie bet whenever he has the edge, and at no other time, then the AP will earn, on average, $3.88 per 100 hands over the long run. The AP will earn $10.52 per 100 hands with the cut card placed at 12 cards. This is not a significant increase in potential income over the 8-to-1 case.
May goes further in his analysis, adding that there are situations when the player can get a much larger edge by using a counting system that end-plays shoes where the last few cards are all ten-valued cards. May states:
“With only tens in the deck you have a 800% edge, since the result must be a tie”
As an exercise, I decided to re-run my simulations to see how often this situation occurs for various cut card placements, and the potential income that can be derived from end-playing a shoe with all ten-valued cards alone. The following table summarizes my results, with cut card placements at 12, 14, 16, 18 and 20 cards: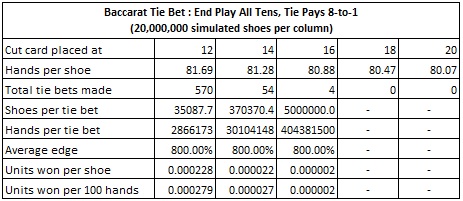
With a cut-card placement at 14 cards, if the AP places $1000 on the Tie bet whenever the remaining cards are all ten-valued (T,J,Q,K), and at no other time, then the AP will earn, on average, $0.027 (2.7 cents) per shoe over the long run. The AP will make one Tie wager every 370370 shoes. Note that no opportunities arose in 20,000,000 shoes to make the Tie bet with a cut-card placement of 18 or 20 cards.
Based on the results of my simulations, I find that May’s system for beating the baccarat Tie bet does not pose a credible threat to casinos. My own work (see this post) shows that no meaningful edge can be gained over the Tie bet by any system that counts any subset of cards. Both ordinary baccarat and the baccarat Tie bet are not vulnerable to a card counting system of advantage play.
In February, 2010, James Grosjean had this to say about John May's system for beating the Tie bet in baccarat (posted on his message board forum at the now defunct www.beyondcounting.com):
"For you to continue to suggest that there is any money to be made counting the Tie bet does a disservice to the community. Your position is based on your stubbornness and refusal to admit that your thesis topic (Tie counting) is in fact a dead-end, but you never had the cold hard numbers to know that in the past. Now those numbers are available, but you don't want to read them … I am quite confident in saying that I have written the last (competent) word on counting the Tie bet in baccarat, and it undermines all of your drivel over the last decade."
Articles, books, videos and posts on card counting baccarat and the baccarat Tie bet are noticed by both sides of the table. Intellectual honesty is paramount.


