I wonder what the future will hold for game protection when devices like Google Glass become part of the mainstream of technological gadgets. In this recent post, I discussed the possibility of baccarat being vulnerable to “perfect play” using an Android app. I showed that if the technologically adept player gets a significant rolling chip rebate, 9-to-1 odds on the Tie bet and deep cut card placement, then he may be able to get enough of an edge to pose a threat. I warned the game protection community to start thinking about this possibility.
I admit that I have my head in the Ivory towers at times. Beating baccarat given these optimal conditions along with the use of technology is a great example. Fortunately, I got “caught” by a reader who obviously lives in the real world. In response to my post on optimal play against baccarat, a reader (Cliff) posed some excellent questions:
So if have the wherewithal to be granted a rolling discount of 1%, the chutzpah to negotiate the Tie bet paid at 9 to 1, no burn cards, how much per hour could I expect to earn with a max bet of say 100k? How would this look to surveillance if we were monitoring the game? I take it that this does not require that the first 80 odd bets be small with the last one or two at table max? From an AP’s perspective how many units per hour could I expect from this strategy if played with enough cover to look like a normal high roller (not massive bet ramp in the last few hands).
Because I am the one creating the hypothetical universe here (one without banjos), not Cliff, I created my own combination of ideal conditions for the technologically adept player. Here is the fantasy game I considered for this analysis:
- Rolling chip rebate of 1.2%
- Cut card at 7 cards.
- No burn cards.
- Tie bet pays 9-to-1
As for how the player actually plays against this game,
- I assume that the Player always wagers optimally – he uses a computer to decide which of the three wagers Player/Banker/Tie has the lowest house edge and that is the wager he always makes.
- I assume the player wagers 1 unit when the casino has the edge.
- I assume the player wagers 4 units when the player has the edge.
The player could do better by Wonging (entering or leaving the game when conditions change). Most card counting experts recommend Wonging for an eight-deck blackjack shoe game. But, a top-tier player is likely playing alone or with a few friends, and he can't very well sit out most of each shoe. I have to assume a "play all" approach. Also, whereas in blackjack a play-all card counter on an eight-deck game would strive for at least a 12-to-1 bet spread, I am assuming a more modest 4-to-1 bet spread.
The following table gives the statistics obtained from a simulation of about 110,000 eight-deck shoes for perfect play against baccarat, when wagering as described above:
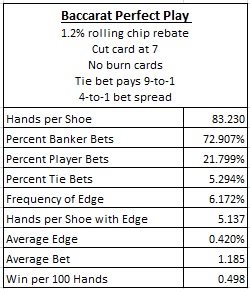
In particular, to answer Cliff’s questions, if the technologically adept player wagers $25,000 when the casino has the edge and $100,000 when he has the edge, then he will win about 100 x 1.185 x $25000 x 0.420% = $12,440 per 100 hands, or about $10,355 per shoe. On average, the player will be wagering $25,000 on about 78 hands per shoe, and $100,000 on about 5 hands per shoe. Naturally, the $100,000 wagers will come late in the shoe.
Cliff then asks some humbling speculative questions:
How would this look to surveillance if we were monitoring the game?
From an AP’s perspective how many units per hour could I expect from this strategy if played with enough cover to look like a normal high roller (not massive bet ramp in the last few hands)?
I don’t think it is possible to fully answer these questions until the technology that makes this type of play possible in a casino actually starts showing up. However, perfect play technology has already been used to beat the Pairs bet (see this post). Here is a sample device (click to enlarge photo):

The following picture is of an Android app that can be used to find the wager Player/Banker/Tie with the lowest house edge. This is available today on the Android market (click to enlarge image).
By itself, beating a rolling chip program outright may not be a realistic goal for the technologically adept player. While the player can get a small edge over the Player/Banker/Tie bets, the need for cover or the presence of poor table conditions could very well negate any possible edge. However, every wager on the table is an opportunity to get an edge. For example, the player can target the Pairs bet, while minimizing his losses against the Player/Banker/Tie bets. The savvy player has options.
Here is a fantasy device. The technologically adept player is playing at the table while wearing Google Glass (or whatever). The device automatically scans the table and identifies the cards and registers their ranks (card recognition technology already exists). The scanned information is input automatically into the combinatorial program (app already exists), which then outputs the current edges for each of the Player/Banker/Tie bets. The program also outputs the edge for the Pairs bet (app already exists) and for other side bets available on the game. The player is automatically fed the current edge for every wagering opportunity at the table. The technologically adept player has a good day.
There is no possible future in which these sorts of devices will not be created. The ongoing problem for baccarat game protection is to be able to recognize what can be accomplished today, while preparing for what will be possible tomorrow. I, for one, am looking forward to a universe without banjos.

A man walked into a bar with his pet alligator and asked the bartender, "Do you serve banjo players here?"
"Sure we do," replied the bartender.
"Good," said the man.
"Give me a beer, and I'll have a banjo player for my alligator."


