There is a variant of baccarat that was brought to my attention last July. This version, called "2-to-1 Baccarat," is non-commission. It has a fairly significant twist in the rules. A three-card winning total of 8 or 9 pays 2-to-1 for bets on the winning side. To balance this extra payout, a bet on Banker or Player loses if the hand ends in a tie.
My first instinct was this variant should be highly countable. Like the Dragon side bet for EZ Baccarat, I thought the winning edge would come from being able to identify situations when hands that use 3 cards are more likely. It turns out that my instinct was wrong.
2-to-1 Baccarat was available at Crown Melbourne casino in Australia. The following documentation contains the game rules on page 21:
Here are how the rules are explained in this documentation:
- If the Player hand comprises three cards which have a total of eight (8) or nine (9) and have a higher point count than that of the cards dealt to the Banker, then winning Player bets pay 2-to-1.
- If the Player hand has a higher total than the Banker hand, (but is not a three-card total of 8 or 9), then winning Player bets pay 1-to-1.
- If the Banker hand comprises three cards which have a total of eight (8) or nine (9) and have a higher point count than that of the cards dealt to the Player, then winning Banker bets pay 2-to-1.
- If the Banker hand has a higher total than the Player hand, (but is not a three-card total of 8 or 9), then winning Banker bets pay 1-to-1.
- If the point count of the cards dealt to the Player hand and Banker hand are of equal value (the hands tie), then wagers placed on the Player and/or the Banker lose.
The following table gives the combinatorial analysis for the house edge and variance for both the Banker and Player bets.
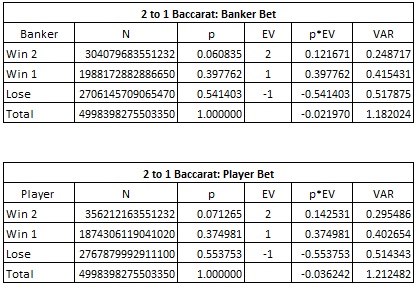
From this we see:
- The house edge on the Banker bet is 2.1970%
- The house edge on the Player bet is 3.6242%
These edges are considerably higher than on the normal game. From a player's perspective, I wouldn't expect this game to succeed. First, losing tie hands will be an objectionable outcome for traditional players. Second, there are already two commission-free baccarat variants that leave the original game essentially intact and keep the house edge low, namely EZ Baccarat (three-card winning 7 is a push) and the version where a Banker winning 6 pays 1-to-2.
As for countability, the usual procedure is to compute the effect-of-removal (EOR) for each card and try to develop a system, then simulate the system to see how it performs. However, there is a method that can be used before any of the work is done to develop a card counting system that gives a practical upper bound to a game's potential vulnerability.
Any card counting system attempts to identify situations where the player has the edge over the house by summing "tags." In practice, these tags are directly related to the EOR for each card. The sum allows the counter to compute a true count. The theory is that when the true count is large enough, then that should correspond to having an edge over the house.
But what if the situations where the player has an edge over the house are rare to begin with? No matter how good the count, the count can't make positive situations occur out of thin air. How can we determine the potential edge?
The approach is to simulate a fixed point in a shoe, somewhere deep just before the cut card, and to see how often an edge occurs at that point, and to quantify that edge. Any card counting system is then limited by this fixed barrier of perfect knowledge. This is the method I used for 2-to-1 baccarat.
I simulated 37217 shoes. For each shoe, I dealt the cards out until 26 unseen cards were left. The specific point when 26 cards are left corresponds to one of the last hands in the shoe. I then computed the exact edge for both the Player and Banker bets on 2-to-1 baccarat at this point in the shoe. I collected these results and imported them into a spread sheet where I conducted further analysis. Here are the results:
- The AP had the edge making the Player bet on 125 shoes (out of 37217). This corresponds to 0.336% of the shoes.
- The average edge making the Player bet was 0.619%.
- The AP had the edge making the Banker bet on 1113 shoes (out of 37217). This corresponds to 2.991% of the shoes.
- The average edge making the Banker bet was 0.731%.
Another way to view these results is graphically. The following graph plots the distribution of player edges for the Player and Banker bets. The horizontal axis (along the bottom) indicates the house edge. The vertical axis (along the left) indicates the frequency that edge occurs. Those portions to the right of 0.00% (in the box) correspond to a player edge. The area under the curves (in the box) indicates the upper bound of potential profit from card counting.
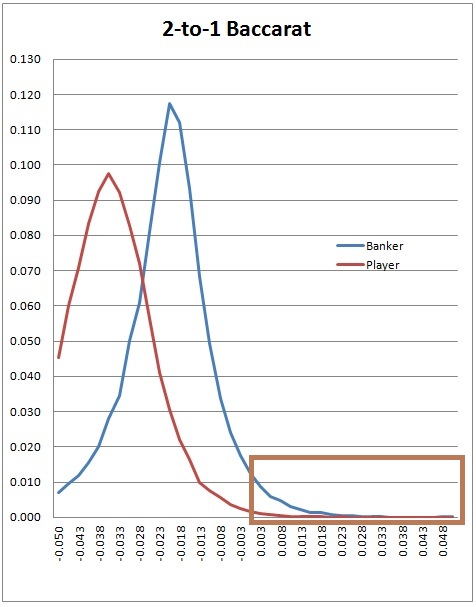
There are two geometric features about this curve I want to point out. These correspond to the average edge when the Banker/Player bet is favorable and the frequency of the opportunity. These are the two numbers that allow the total potential income to be computed.
First, if you consider the portion in the box under each curve, then the "center of gravity" of each curve corresponds to the average edge. Thus, the area under the blue curve in the box has "center of gravity" at 0.00731. The area under the red curve in the box has "center of gravity" at 0.00619.
Second, the total area under each curve is exactly 1. The fraction of the entire curve that is in the box corresponds to the frequency that the opportunity to make the wager occurs. Thus, the area under the blue curve in the box is .02991. The area under the red curve in the box is .00336.
The point of any card counting system is to try to identify when the remainder of the shoe corresponds to a player edge. No card counting system can do better than perfect play. And perfect play is bounded by the indicated area. In other words, there is very little profit there.
In light of this graph, when I computed the EORs, it came as little surprise that these values were very small compared to the edge that must be overcome. Recall that the baseline edge for the Banker bet is 2.197% and for the Player bet it is 3.624%:
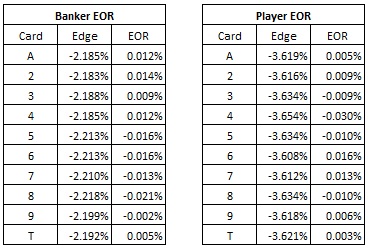
My conclusion is that 2-to-1 baccarat is not vulnerable to card counting.


