I have recently been obsessing over computer-perfect play against the baccarat Tie bet and Pairs bet. Almost 18 months ago, I gave a rough estimate for the earnings possible from computer-perfect play against baccarat, which I presented in this post. However, that research definitely left room for improvement (will my laziness never end?). The current post takes computer-perfect baccarat to the next level. I am going to give the computer-perfect win-rates and other statistics for each of the Player, Banker and Tie bets for a variety of cut card placements. This will allow me to give an overall win-rate for a patron using a computer to play baccarat perfectly.
Computer-perfect play means keeping track of the exact house edge on each of the Player, Banker and Tie bets each round, based on the exact composition of the cards left in the shoe. The player then makes a wager on a specific bet whenever he has the edge over the house on that bet; otherwise the player just sits on his hands and waits. The point of an analysis such as this is to put an absolute upper-bound on the win-rate from ordinary advantage play against baccarat using methods such as card counting. This analysis does not cover more sophisticated methods, such as location play, hole-carding or edge sorting.
The question of card counting at baccarat comes up often when casino management considers game protection issues for the game. The fact is, card counting can never do better than computer-perfect play. Card counters use a counting system designed to give a rough idea when the player has an edge; however, card counting cannot create an edge where none exists. It follows that card counting is a weak approximation of computer-perfect play, and therefore is less profitable than computer-perfect play. Nevertheless, there is no end of flimflam devoted to the topic of card counting baccarat. All such work is either intellectually dishonest or misguided. In either case, it is unsound.
Here is a sampling of baccarat card counting nonsense:



To continue on, this analysis assumes an eight-deck shoe. We assume the game uses the following standard burn-card and cut card rules:
- A card is dealt and exposed at the start of the shoe.
- Based on the value of that card an additional number of unseen cards are burned.
- If a Jack, Queen or King is exposed, then 10 cards are burned, otherwise, the number of burned cards equals to the pip value of the exposed card.
- If the cut card is dealt mid round, then one additional round is dealt.
- If the cut card is the first card dealt in a round, then two additional rounds are dealt.
With these rules, the cut card can be placed no less than 12 cards from the end. If the exposed card is an Ace (so that there is one unseen burned card) and the cut card is set at 12 cards, then it is possible that in the final round, there are only six cards remaining in the shoe (seven unseen cards). If the final round takes six cards, then the shoe will be entirely depleted. I will consider cut card placements from 12 cards to 26 card (1/2 deck). I also give results for cut card placements at 39 cards (3/4 deck) and 52 cards (1 deck).
The following tables give the statistics from simulations of computer-perfect play against the Player, Banker and Tie bets. The statistics given in each row were obtained by a simulation of one hundred million (100,000,000) baccarat shoes using computer-perfect play.
I begin with the Player bet:
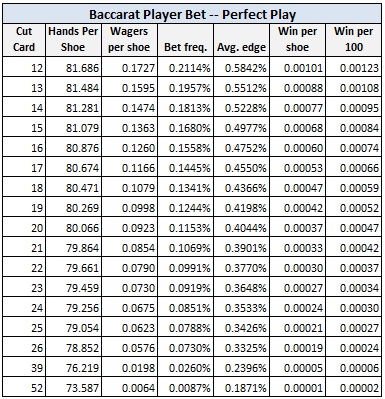
For example, with the cut card placed at the standard location of 14 cards, with computer-perfect play against the Player bet:
- The player will make a bet on average once per 6.78 shoes.
- With a $1000 wager whenever the player has the edge, and otherwise no wager, the player will earn about 95 cents per 100 hands using computer-perfect play.
Here are the results for the Banker bet:
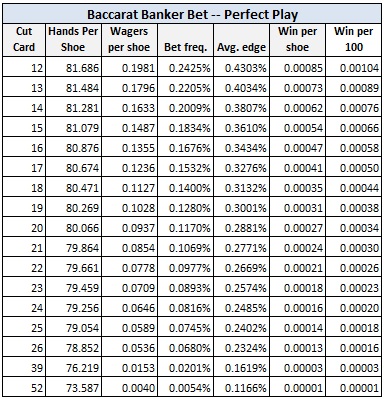
For example, with the cut card placed at the standard location of 14 cards, with computer-perfect play against the Banker bet:
- The player will make a bet on average once per 6.12 shoes.
- With a $1000 wager whenever the player has the edge, and otherwise no wager, the player will earn about 76 cents per 100 hands using computer-perfect play.
It follows that if a player is using a card counting system to target the Player/Banker wagers in baccarat, then that player’s maximum win-rate cannot exceed $1.71 cents per 100 hands making $1000 wagers (17.1 cents per 100 hands with $100 wagers).
Although I covered computer-perfect play against the Tie bet in this post, it was no extra effort to redo that work as part of these simulations. Here are the results for the Tie bet:
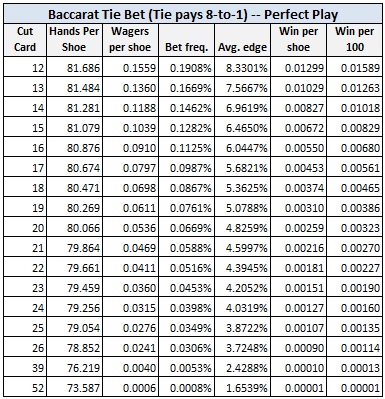
For example, with the cut card placed at the standard location of 14 cards, with computer-perfect play against the Player bet:
- The player will make a bet on average once per 8.42 shoes.
- With a $1000 wager whenever the player has the edge, and otherwise no wager, the player will earn about $10.18 cents per 100 hands using computer-perfect play.
Finally, here are the combined results for computer-perfect play against the combination of opportunities Player/Banker/Tie:
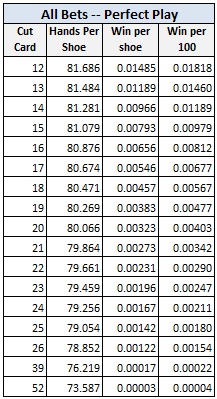
For example, with the cut card placed at the standard location of 14 cards, with computer-perfect play against the Player/Banker/Tie bets:
- With a $1000 wager whenever the player has the edge, and otherwise no wager, the player will earn about $11.89 cents per 100 hands using computer-perfect play ($1.19 per 100 hands with a $100 wager).
- The computer-perfect baccarat player will make about 1 wager every 7 shoes on the Player bet, 1 wager every 6 shoes on the Banker bet, and about 1 wager every 8.5 shoes on the Tie bet.
- The player is going to sit out a lot of hands. That will give him plenty of time to buy a cup of coffee per day with the proceeds from his perfect play.
Surely I will write another article at some future time, trying once again to settle the matter of card counting baccarat. For now, the numbers above tell the story. Forget about it. Baccarat has some real game protection issues, but card counting is not one of them.


