In this post I am going to give the win-rate statistics against the Tie bet using computer-perfect play. In this analysis, I assume the AP is keeping track of the cards that have been played from the shoe. Before the start of each round, the AP uses a computer to give him the exact edge on the Tie bet based on the knowing the composition of the cards left in the shoe. If the AP has the edge over the house, he makes a Tie wager; otherwise he does not place a wager. These results give an absolute upper bound on the earning potential against the Tie bet through ordinary advantage play.
Of course, if the player knows a slug of cards through shuffle tracking or by some nefarious means, he can achieve a huge edge. Likewise, the AP can beat the Tie bet if he is edge sorting and has the full view of the backs of the first four cards before placing his wager. But that’s not what this post is about. Computer-perfect play takes into consideration all of the normal means an AP has of gaining an edge, including ordinary card counting and so-called "end-plays." It doesn’t matter what the AP thinks he knows or how good he thinks his system is, the AP is not going to outperform computer-perfect play. While some wayward authors have tried making deep waters out of this topic, the Tie bet is barely a dripping faucet. Those who preach otherwise are either flimflam artists or misguided (for example, see this post).
This analysis uses the following standard burn-card and cut-card rules:
- A card is dealt and exposed at the start of the shoe.
- Based on the value of that card an additional number of unseen cards are burned.
- If a Jack, Queen or King is exposed, then 10 cards are burned, otherwise, the number of burned cards equals to the pip value of the exposed card.
- If the cut-card is dealt mid round, then one additional round is dealt.
- If the cut-card is the first card dealt in a round, then two additional rounds are dealt.
With these rules, the cut-card can be placed no less than 12 cards from the end. If the exposed card is an Ace (so that there is one unseen burned card) and the cut card is set at 12 cards, then it is possible that in the final round, there are only six cards remaining in the shoe (seven unseen cards). If the final round takes six cards, then the shoe will be entirely depleted. I will consider cut-card placements from 12 cards to 26 card (1/2 deck).
Computer-Perfect Play: Tie pays 8-to-1
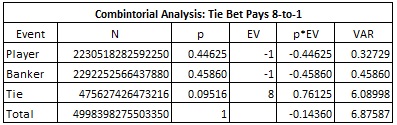
I begin with the case when the Tie bet pays 8-to-1. This is the most common version world-wide. The following table gives the combinatorial analysis for the Tie bet in this case, showing a house edge of 14.36%:
Here are the statistics from simulations of computer-perfect play against the Tie bet. The statistics given in each column were obtained by a simulation of one hundred million (100,000,000) baccarat shoes using computer-perfect play:
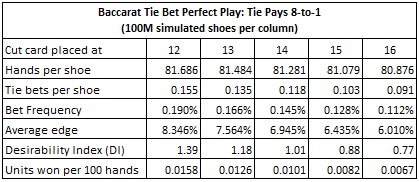
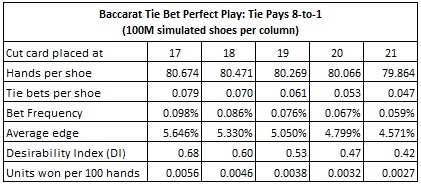
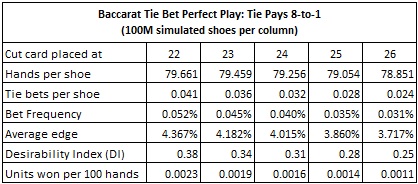
For example, with the cut-card at the standard placement of 14 cards, then the computer-perfect AP will earn 0.0101 units per 100 hands. If this AP wagers $100 whenever he has the edge and otherwise does not make a wager, then he will earn approximately $1.01 per 100 hands.
Note also that with the cut card placed at 14 cards, the AP makes 0.118 Tie bets per shoe. That is equivalent to one Tie bet every 8.47 shoes. At a pace of 80 minutes per shoe, the AP makes a Tie bet about once every 11.5 hours. That's going to look funny.
Perhaps the most significantly discouraging result for the AP is the DI (desirability index, see this post and this post). In general, when the DI is less than 6, the game is considered borderline playable. With a DI of 1.01, the Tie bet is simply not interesting to advantage players.
Computer-Perfect Play: Tie pays 9-to-1
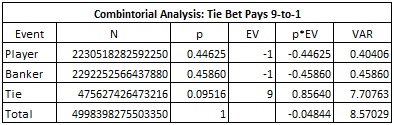
I next consider the case when the Tie bet pays 9-to-1. This payout is very rare. The following table gives the combinatorial analysis for the Tie bet in this case, showing a house edge of 4.84%:
Here are the statistics from simulations of computer-perfect play against the Tie bet. The statistics given in each column were obtained by a simulation of one hundred million (100,000,000) baccarat shoes using computer-perfect play:
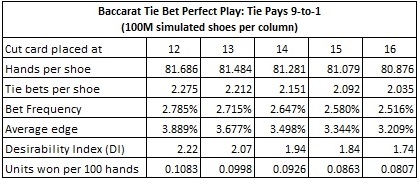
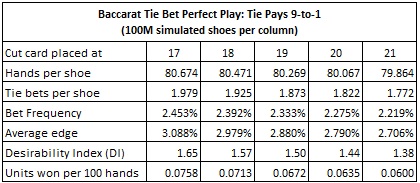
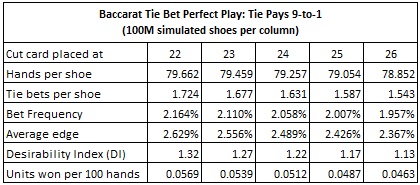
With the cut-card at the standard placement of 14 cards, then the results above show that computer-perfect AP will earn 0.0926 units per 100 hands. If this AP wagers $100 whenever he has the edge and otherwise does not make a wager, then he will earn approximately $9.26 per 100 hands. In this case, the DI is 1.94, which is still well below the threshold of a playable opportunity for the advantage player.
I first wrote about beating the baccarat Tie bet using computer-perfect play when it pays 9-to-1 in this post. With the cut-card at 14 cards, my estimate was that Tie bet earnings per shoe were at most 0.094 units. I was a bit lazy in that post, but I did achieve an upper bound that I felt comfortable with. After the considerably more refined simulation above, my new upper bound is 0.0753 units per shoe (0.0962 units per 100 hands).
My opinion is that the Tie bet, whether it pays 8-to-1 or 9-to-1, is not a meaningful advantage play opportunity.


