Edge sorting in baccarat takes place when the player can observe the back of one or more cards before making his wager (see this post for an introduction). If the player is able to sort the cards, then this knowledge allows the player to gain an edge. As I showed in this post, the ability to see one sorted card allows the player to gain an edge of 6.765% over the house. In this post, I showed that if the player can see the first four cards, then he can gain an edge of 20.928% over the house. However, I made a very naive assumption in the four-card analysis when I used the same sorting groups for four cards that I used in the one-card case. I recently received an email from a reader who rocked my baccarat edge sorting world. He showed me that the sorting groups for the four-card case could be improved, giving the edge sorter an astronomical advantage of 30.291% over the house. Wow!
I must begin by thanking this individual, Fred Roach, for his outstanding work. Fred's email indicated that he had written a computer program that analyzed every possible sorting group in the four-card case. That’s 1023 different sorts. He sent me a spread sheet showing the best sort he found. After seeing what Fred demonstrated, I did my own analysis from scratch and quickly confirmed Fred’s key results. After a few emails back and forth, Fred and I agree on pretty much everything. This post presents Fred's new findings on optimal sorting groups for four-card sorts in baccarat.
As a reminder, the sorting groups that are used when the AP has top-card (first-card) information are High = {6, 7, 8, 9} and Low = {0, 1, 2, 3, 4, 5}. In this case, the AP wagers on Banker if the top card belongs to the Low group and Player if the top card belongs to the High group. This results in an edge over the house of 6.765%. My mistake was to assume these same High/Low groups should be used in the four-card case.
The following table shows the edge the AP can gain for nine different High/Low sorting groups:
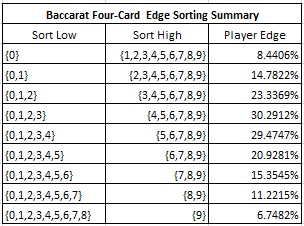
It follows that the best sort to use when four-card information is available is Low = {0, 1, 2, 3} and High = {4, 5, 6, 7, 8, 9}. The following table gives the full combinatorial analysis for this optimal sort, showing an edge for the AP of 30.2912%:
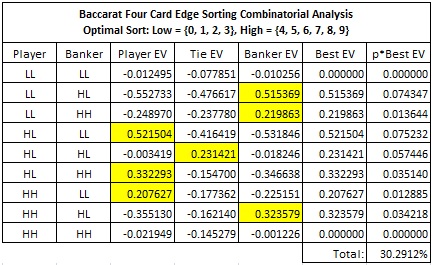
The cells in yellow indicate optimal strategy. Note that in two situations (LL vs. LL and HH vs. HH), no advantageous wager can be made by the AP.
By reference to this combinatorial analysis, note that:
- The player will wager on Player on 31.207% of the hands.
- The player will wager on Banker on 31.207% of the hands.
- The player will wager on Tie on 24.823% of the hands
- The player will make no wager on 12.764% of the hands.
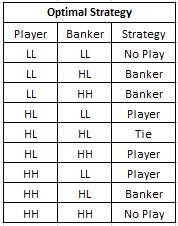
The following table gives simplified four-card edge sorting strategy, using the optimal four-card sort given above:
If you want to do your own exploration of the edges that are possible using various sorting schemes, or you want to verify my results, everything you need for these computations is contained in the following spread sheet:
Baccarat_Four_Card_Edge_Sorting_Data
The optimal four-card sort is demonstrated for one of the most commonly used cards in the following image:
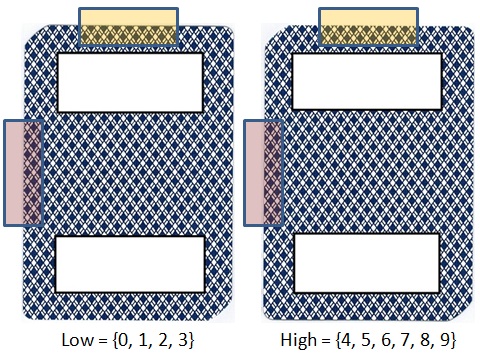
When the initial four cards are dealt face down, the AP may see something like the following, corresponding to Low, High vs. High, High (click on this image to make it larger):

The following picture illustrates how this grouping can occur in live play, where the Player hand is (0, 9) and the Banker hand is (6, 8). If the first four cards are dealt face down before the AP makes his wager, and the cards have been sorted according to the optimal High/Low groupings above, then the AP has a 33.23% edge over the house if he bets on Player.

Does Chung Sun (the Asian lady who assisted Phil Ivey, the so-called “Queen” of sorts) use the optimal sort, or does she use the standard {0, 1, 2, 3, 4, 5} vs. {6, 7, 8, 9} sort when she accomplishes the four-card sort against her casino targets? That’s one question I would love to have answered. Anyone?
I believe this is the end of the story as far as presenting an optimal four-card sort for the main game. Fred also found a sort that optimized both the main game and the Pairs bet simultaneously. I once again want to thank Fred for his impressive work and his generosity in sharing his results with me.


