I recently received an e-mail from an individual at an overseas casino, asking if I would review his casino's baccarat loss rebate program for advantage play vulnerability. Like many similar programs, it included not only the standard loss rebate, but also incentives like airfare, room, food & beverage, and agent's commission. What distinguished his program was that there was no minimum play required to cash out the loss rebate. A player could play for 5 minutes, cash out, play another 5 minutes, cash out, and so on. His question was simple: could a player beat him. My answer is equally simple: yes.
Baccarat is a very robust game as far as loss rebates go. It has very low variance compared to its relatives, blackjack, roulette and craps. It also has a very low house edge, second only to blackjack. It is rare for players to go through large bankroll swings -- the very kind of swings that give loss rebates value for the AP. The longer that a player is at the table, the more the "long run" comes into play, negating the value of a loss rebate program. Because of these factors, I didn't expect to find much AP value. However, in the unique case when a player can cash out a rebate with no minimum play requirement, loss rebates can generate significant income for the highly bankrolled AP.
To investigate the profit potential, I followed the same model that I used to investigate roulette in this post and this post, and blackjack in this post. That is, I determined optimal stopping points that maximized the players average net win. These stopping points are the loss-exit-point and the win-exit-point: the two goal posts that instruct the player to either stop and collect a loss rebate, or to stop and book a win.
The rebates I am going to consider have percentages 10%, 12%, 15%, 18% and 20%. The only constraints on this player are his win/loss stopping points. I am going to assume the AP makes all of his wagers on Banker, with a house edge of 1.06%. As usual, to determine the optimal stopping points, I ran a lot of simulations. For each rebate percentage, I simulated combinations of possible win-exit-points and loss-exit-points. For each combination of exit points, I ran ten million (10,000,000) simulated high-limit players. I then averaged together the results for these ten million players to get the average result for a player with the given exit points. By reviewing all of this data, I determined the specific win/loss exit-points that optimize the average net win for the player.
The following table summarizes my analysis of loss rebate advantage play for a player who is making a $100,000 bet on Banker in baccarat:
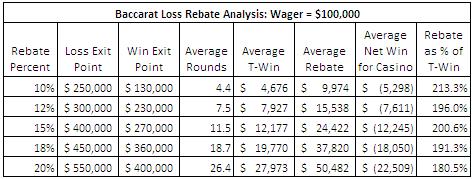
A fast-paced baccarat table runs at a pace of about 70 hands per hour. If an AP finds a game that gives a 20% loss rebate on losses in excess of $500,000, then on average he will play 26.4 hands, or about 23 minutes, before he hits an exit point. For his 23 minutes of work, he will earn about $22,500. If an AP is allowed to cash out with no time requirement, then he will quickly amass a fortune. This is exactly the scenario that Don Johnson exploited in blackjack, in much the same way.
Many loss rebate programs have a tiered structure. The actual percentage rebate the casino pays is based on the total loss the player accrues. In this case, there is always a tier that optimizes the AP's average net-win, and the player will use that tier's loss rebate percentage as the basis for determining his loss-exit-point. These tiers may also include graduated incentive values in other categories, including increased airfare, food & beverage and others. To do a full analysis requires taking all of these factors into consideration.
There are a number of ways to protect baccarat from loss-rebate style advantage play:
- Watch for players who play hit-and-run style.
- Watch for players who leave after small wins, but continue playing through larger losses.
- Change the discount policy to require a minimum playing time to be eligible for a loss rebate.


