Baccarat and blackjack have one important commonality: the house edge for each changes as cards are played from the shoe. The advertised house edge is based on the initial composition of the shoe, but that value is not fixed throughout the game. In the case of blackjack, the house edge swings in favor of the player on about 30% of the hands, making card counting a viable strategy for the advantage player. As I showed in this post and this post, things are not quite as easy for the baccarat player. But that doesn't mean that gaining an edge is impossible.
Baccarat players often study scoreboards showing historical results to help them predict the result of the current hand. All betting systems based on these illusory patterns are worthless. There are no patterns. There is no information that the outcomes of previous hands provides that can be used to improve the odds for the current hand. However, the lack of historical implication does not mean that an optimal betting system does not exist. Indeed, on any given hand, one of Player, Banker or Tie will have the lowest house edge.
Suppose a baccarat player has the ability to know which of the three wagers, Player, Banker or Tie, has the lowest house edge each hand. Given this knowledge, assume the player always makes the best bet. On the first hand of the shoe, the edges for each wager are just the advertised house edges and the player would make a Banker bet. But as cards are dealt and the cards in the shoe are depleted, these three edges change. The "system" player can do no better than to always choose the wager with the lowest house edge. This method of wagering is what I mean by the "world's greatest baccarat betting system." For brevity, I will refer to this betting system as "optimal wagering."
At first, optimal wagering may seem like fantasy – how could a player possibly know which wager (Player, Banker or Tie) has the lowest house edge each round? Recently, I became aware of an APP for Android-based smart phones that allows the player to compute the exact house edge for the Player, Banker and Tie bets at any point in the shoe. To use it, the player enters cards as he observes them being dealt. Before each round, the player presses the “compute” button. After a moment, the screen shows the precise returns for each bet. I double checked the results produced by this APP in a couple of cases; the creators appear to correctly use standard combinatorial methods to compute the returns.
Go to the Android “Play Store” and search for “baccarat card counting.” Here is a link that gives the details:
https://play.google.com/store/apps/details?id=com.proware.baccaratcardcounting&hl=en
Here is a screen shot of the home page for this APP (click on the image to make it larger):
Using this APP is not the only way optimal wagering can be successfully implemented. In some casinos, high-rollers are allowed to play by phone. The cards dealt and result of each hand are relayed to the player as the shoe proceeds. Such a player could certainly use the APP above, or he could use his own customized software, to obtain the edge for each wager. With easily available technology, optimal wagering is a very real possibility.
To quantify the effect of using the world's greatest baccarat betting system, I performed a simulation of 200,000 eight-deck shoes. Here are the assumptions made in the simulation:
- The cut card is placed at 14 cards, with the usual burn card and cut card rules.
- The Tie bet pays 9-to-1.
- The player always makes the wager (Player, Banker, Tie) with the lowest house edge each hand.
- The player’s wager is fixed throughout his play (1 unit).
Here are the results of the simulation:
- The house advantage is 0.878%.
- Player is the best wager on 20.77% of the hands.
- Banker is the best wager on 75.51% of the hands.
- Tie is the best wager on 3.72% of the hands.
- The player loses, on average, once every 2.15 hands.
The improvement in house advantage to 0.878% is far from sufficient to beat the house: the player needs a lot more. In the case of a high-roller, more is frequently available. Most high-rollers are enrolled in some type of rolling chip program (see this post), where they are paid a percentage rebate based on the number of rolling chips lost.
The following table shows the house advantage for a player using optimal wagering, based on various rolling chip rebate percentages:
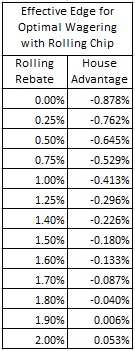
Rebates between 0.75% and 1.25% are quite common internationally. I personally know of a case of a high roller getting a 1.6% rolling chip rebate. Anecdotally, I have heard of rolling chip rebates in excess of 2.0%. A rolling chip rebate of 1.90% gives the player who is flat betting and using optimal wagering an edge over the casino.
The player who is combining technology with a rolling chip incentive program can do much better. If the player uses a “bet spread,” making larger wagers whenever the house edge is smaller, then he can significantly improve his results. To see the effect of using a bet spread, I performed a simulation of 150,000 shoes, with the following assumptions:
- The cut card is placed at 14 cards, with the usual burn card and cut card rules.
- The Tie bet pays 9-to-1.
- The player always makes the wager (Player, Banker, Tie) with the lowest house edge each hand.
- The player wagers 1 unit if the lowest house edge is 0.90% or greater.
- The player wagers 10 units if the lowest house edge is less than 0.90%.
- The player is not playing with a rolling chip program.
With these assumptions, the results of the simulation are as follows:
- The player wagers, on average, 2.70 units per hand.
- The house advantage (totalWon/totalWagered) is 0.38%.
The effect of a bet spread on the house advantage is striking. This low edge of 0.38% can now easily be overcome with a modest rolling chip rebate.
I performed a simulation of 150,000 shoes with the same assumptions as above, except that I assumed the player received a 1% rolling chip rebate. With these assumptions, the results of the simulation are as follows:
- The player wagers, on average, 2.70 units per hand.
- The player advantage (totalWon/totalWagered) is 0.11%.
These numbers show that the player is beating the house outright. For example, with a $1000 unit, the player will wager $1000 x 2.70 x 100 =$270,000 per 100 hands. With a 0.11% edge, this leads to a profit of $297 per 100 hands.
I note that I have not attempted to optimize the profitability of this method. The computation above is simply intended to show the possibility of getting an edge. A larger spread across a wider range of percentages will certainly improve the player's return, as will a higher rolling chip rebate. I leave the details to the interested reader.
In my opinion, effective game protection for baccarat must include the assumption that every call-in player is using some sort of computer technology to assist with his decision-making. A routine audit can determine if a player is using optimal wagering. As smart phone APPs like the one given above become more powerful and easier to use, it will become increasingly necessary to scrutinize players on the floor who are playing with rolling chip incentives to insure that the house still has the edge.


