In this post I considered ordinary blackjack card counting (BJCC) for six decks. The purpose of that post was to compare BJCC to card counting the various side bets for the six-deck shoe game. This post presents the analysis for the two-deck game. I wish to express my thanks to Norm Wattenberger, who assisted in this analysis by running a simulation of the two-deck game on his excellent software, Casino Verite.
This article follows the template of the six-deck article. I am simply going to substitute the results for the two-deck case into the text of the six-deck article, leaving the discussion mostly unedited.
One way to view BJCC is that the main game of “blackjack” is its own side bet. In this case we imagine a player who is watching a table with one player on it, and whenever the count hits the trigger, he wagers $100 behind the player on the table. In its pure form, this is the most direct comparison. The AP is either wagering $0 or $100 on BJCC.
In practice, blackjack-as-a-side-bet does not happen. Therefore, I also analyzed the case when the player wagers $5 below the trigger count and then makes an additional $95 wager on “blackjack” when the count is at +1 or above. In other words, this AP is spreading $5 to $100.
For an AP with a maximum bet of $100, these two methods of play will generate the maximum profit possible for the AP, regardless of the counting system he uses or the number of indices he uses. This is the “binary” approach. Either bet $0/$100, or bet (table minimum)/$100. No bet ramp. No Kelly. No ROR. Just pure profit-potential.
In this analysis, I assumed the player was using the High-Low card counting system and all card-counting indices for varying his play. This is a perfect counter.
I assumed that the blackjack rules were standard:
- Two decks, cut card placed 29 cards from the end
- Dealer hits soft 17
- Player can double on any first two cards
- Player can double after split
- Split aces receive one card each
Norm ran a simulation of 718,194,064 two-deck shoes for me. I used Norm’s data to cull the comparative results for BJCC vs. side bets.
The full data Norm provided to me is available here:
BJCC_12_11_12
The following table gives the analysis of the “blackjack-is-a-side-bet” AP. This is the AP who is watching a table with one player on it, and whenever the count hits the trigger, he wagers $100 behind the player on the table, otherwise he makes no wager.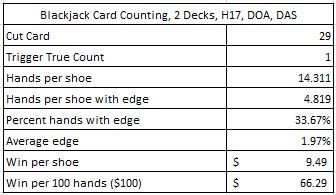
To get the net win for the AP who is using the “play-all” approach, it is sufficient to quantify the hands where the house has the edge and subtract. The following table gives details of the hands where the house has the edge and the AP is wagering $5 per hand: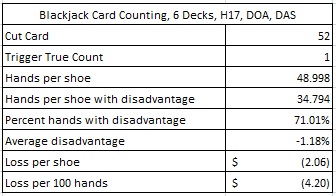
The following table summarizes the net win for the play-all AP. These values are obtained by combining the results from the two tables above:
In summary,
- The “blackjack-is-a-side-bet” AP is earning $66.29 per 100 hands.
- The “play-all” AP is earning $62.13 per 100 hands.
These amounts are the maximum earnings possible for a card counter using the High-Low system. There is simply no way to earn more with a maximum wager of $100 from BJCC. This leads to an extremely useful result for the game protection community.
Theorem Assume an ordinary blackjack card counter using High-Low. The game is standard, 2D, H17, DOA, DAS. The cut card is set at 52 cards. If the AP’s maximum wager is $Z, then the AP’s maximum win rate is:
Maximum win rate = $62.13 x (Z/100), per 100 hands.
For example, if a suspected card counter is making a $2,000 maximum wager, then his maximum win rate is:
$62.13 x (2000/100) = $1242.60, per 100 hands.
The following table gives comparative win-rates for BJCC and the side bets I’ve analyzed in this blog to date.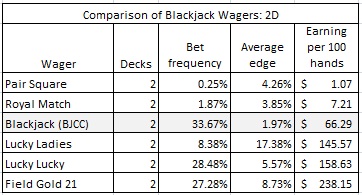
Note that BJCC has the lowest average edge of all the wagers in this table. On the other hand, BJCC has the highest bet frequency (except Slingo). Every other wager in this table has a lower bet frequency and higher average edge.This underscores the high volatility the ordinary card counter experiences: a high frequency of wagers with a razor-thin edge.
The results in this table are the best possible for BJCC. In practice, the AP will earn at a substantially lower rate. It is immediately clear that BJCC is, at best, a mediocre opportunity for the AP.


