When I heard Don Johnson (DJ) speak at the World Game Protection Conference last Tuesday, I expected him to dismiss his blackjack winnings as the result of a little bit of advantage play and a lot of luck. That’s how he portrayed events in this article in Atlantic Magazine. However, after his explanation of how he beat horse racing (see this post), there was little doubt about his skill as one of the world’s top advantage players. When DJ smoothly quoted the exact house advantage of one of the blackjack games he played (0.263%), he removed all doubt.
If you have not yet seen it, I recommend this video produced by Bloomberg [added January, 2014]. It gives a good feeling for who Don Johnson is, as a person. Factually, it is better than most mass consumption articles on gambling, but still falls very short from giving any real explanation for what happened.
As DJ explained, the deal he negotiated in Atlantic City had the following terms:
- DJ placed $1,000,000 in credit with the casino.
- Any time DJ lost $500,000 in a day, he could stop playing and receive a 20% rebate on his loss.
- He could place a maximum wager of $100,000. Some places, this maximum was $50,000.
In the casino-world, it is often the case that people state something “obvious” which is in no way “obvious” and is often just wrong. Such was the case in the aftermath of DJ’s slaughter. Almost everyone took it for granted that the best strategy was for DJ to play until he either won $500,000 or lost $500,000, then leave for the day. This “strategy” appears logically sound (if you're not using any logic). But, strangely, it didn’t represent the actual course of events in DJ’s play. In fact, DJ played much longer on the days he was winning than this “strategy” dictated. On losing days, DJ often endured a loss of more than $500,000. I decided to model the circumstances of DJ’s play to determine the optimal stopping points. What I found showed that DJ was right to continue playing well beyond the mythical “stopping points” of +/- $500,000.
First, I fixed the game played. For top players, the following rules are standard on a shoe game:
- Six decks
- Dealer stands on soft 17
- Player can double on any first two cards
- Player can double after split
- Player can re-split aces
- Player can re-split to four hands
- Late surrender.
DJ certainly played this game. He may have played against other rule-sets, but he did not disclose those.
Next, I wrote a computer program that allowed me to do a Monte Carlo simulation of possible stopping strategies used by DJ. This simulation actually modeled a shoe-game that used a cut card with the rules listed above. It is a bit of arcane science, but when the dealer uses a cut card, the edge moves slightly towards the house side (the so-called "cut card effect"). In the case of this game, the edge is about 0.29% using a cut card. For more details, I refer you to blackjack appendix 4 at the Wizard of Odds website.
I then ran 16 simulations for various stopping strategies (from a $500,000 win up to a $2,000,000 win) to determine the optimal stopping point (rounded to $100,000). Each of the 16 simulations consisted of modeling one hundred million (100,000,000) players using that stopping strategy, and averaging their results. The program's output included the player’s edge over the house, the expected win for the player, and the average number of hands played by the player.
The following table gives the results of the analysis of the stopping points for DJ with a $100,000 flat wager:
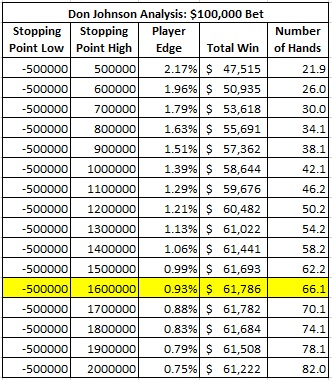
These results show that the optimal stopping point for DJ was a win of $1,600,000 (not $500,000, as is popularly believed). DJ was playing with an overall edge of 0.93% over the house. DJ’s expected win was $61,786. The expected number of hands played was 66.1.
The following table gives the results of the analysis of the stopping points for DJ with a $50,000 flat wager: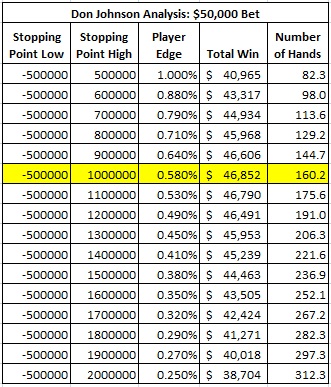
In this case, the optimal stopping point for DJ was a win of $1,000,000. DJ was playing with an overall edge of 0.58% over the house. DJ’s expected win was $46,852. The expected number of hands played was 160.2.
At this point you may also wonder at the credibility of stopping with a loss of $500,000, and you would be right. Once again, popular belief is misguided. After DJ lost $500,000, he is essentially playing with a discount of 20% on every bet he makes, since he no longer has to qualify for his loss discount. The only constraint is that DJ should keep enough to make a double down or split ($200,000 with a $100,000 bet and $100,000 with a $50,000 bet). DJ clearly stated in the talk that on several occasions he lost more than $500,000 before quitting for the day. Do you think DJ knew what he was doing?
With two degrees of freedom (high and low stopping points), I re-did the analysis given in the tables above. In the results below, I assumed $1,000,000 put in the cage, no more, no less. In my next article on Don Johnson (see this post), I waive this requirement as well to find Johnson's optimal win-rate based on unrestricted win/loss-quit points.
Here are the optimal stopping points and other pertinent data when wagering $100,000 per hand, assuming $1,000,000 in the cage:
- Stop when the current bankroll is less than $200,000 (losing more than $800,000).
- Stop after winning $2,000,000.
- The player edge is 0.63%.
- The average total win is $85,800.
- The average number of hands is 136.9.
Here are the optimal stopping points and other pertinent data when wagering $50,000 per hand:
- Stop when the current bankroll is less than $100,000 (losing more than $900,000).
- Stop after winning $1,200,000.
- The player edge is 0.34%.
- The average total win is $59,900.
- The average number of hands is 350.3.
There is another approach to this analysis. Suppose DJ plays without stopping points, but instead pre-determines the number of hands he is going to play per day and sticks to that number, no matter what. Subject to a fixed number of hands, what number of hands would maximize DJ’s winnings? In this case, the analysis is nearly exact. The methodology is described in the book “Casino Operations Management,” chapter 15. I previously wrote a version of this analysis for my own consulting work and that's what I used to model DJ here. I simply input his loss rebate parameters and manually tried various numbers of hands until I found his maximum win.
The following table gives the optimal “number of hands” stopping point for a $100,000 wager:
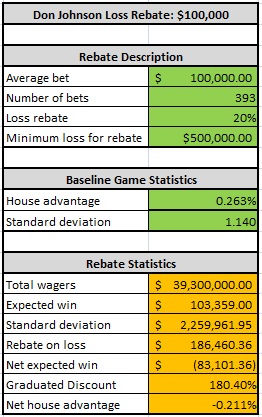
With a $100,000 flat-bet and a “number of hands” stopping point, DJ should play exactly 393 hands per day. In this case, DJ would average winning $83,101 per day, with an average edge of 0.211% over the house.
The following table gives the optimal “number of hands” stopping point for a $50,000 wager:
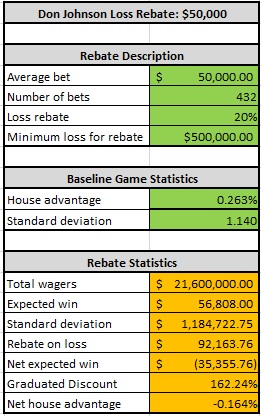
With a $50,000 flat-bet and a “number of hands” stopping point, DJ should play exactly 432 hands per day. In this case, DJ would average winning $35,356 per day, with an average edge of 0.164% over the house.
This data is not the end of the story to explain how DJ crushed the house. During his talk, DJ explained that he got $50,000 show-up money per day. He also stated that he crafted an extremely belligerent and obnoxious personality that pushed dealers and staff to the edge. He stated that this contributed to dealer errors and judgement calls made by floor staff. He estimated that he won an extra three units per day by virtue of his “act.” That amounted to either $150,000 or $300,000 based on his wager size (I take DJ at his word on this, I cannot verify these numbers).
Finally, DJ revealed that he had secret teammates. He said that the table limits were from a table minimum of $100 to his flat bet (either $50,000 or $100,000). Whenever the shoe went sufficiently negative, he would throw some sort of “fit” consistent with his act and stop playing. His teammates would then eat the remainder of the negative shoe. In this way, his play was the same as a card counter who effectively spread his bets from $100 to DJ's maximum bet of either $50,000 or $100,000. I estimated DJ’s additional earnings per day from blackjack card counting by using the values given in this post. Using that analysis,
- With a $50,000 bet, DJ had a theoretical win of about $26,000 per day from card counting.
- With a $100,000 bet, DJ had a theoretical win of about $21,000 per day from card counting.
Taking all these sources of income into consideration, DJ’s expected earnings per day with a $50,000 flat-bet was approximately:
- $60,000 + $50,000 + 3x$50,000 + $27,000 = $287,000.
DJ’s expected earnings per day with a $100,000 flat-bet was approximately:
- $86,000 + $50,000 + 3x$100,000 +$21,000 = $457,000.
In the article in Atlantic Magazine, it appeared that DJ had been incredibly lucky to win as fast as he did. It is now clear that there was very little luck involved. DJ manipulated the “market conditions” he was provided to create conditions he could beat. DJ then consulted with his mathematical advisers to help create a strategy to optimize his return given all the available parameters of play. DJ then implemented his plan with an extraordinarily high level of talent that spanned every strategic and tactical nuance.
It is humbling, no matter which side of the tables you play, to witness this level of skill, planning and execution. The casinos in Atlantic City didn’t stand a chance.


