I received the following question from a reader:
There is a current policy involving Blackjack payouts and insurance at my casino. When a player has a natural 21 and betting a 50¢ piece they are paid $1 opposed to 75¢ due to not having 25¢ cheques. Also when a player has a bet of say $5.50 and they insure for $2.50 and win the insurance bet they are paid the 2-to-1 as well as keeping the 50¢ cheque of their initial blackjack bet since they, due to the lack of 25¢ cheques, cannot insure for full. The question I pose to you is with this policy how much does this cut into the house edge on Blackjack?
The first scenario the reader states refers to a 50 cent wager on blackjack, where the casino pays $1 instead of 75 cents on a player-blackjack. This is the same as blackjack paying 2-to-1. Excluding blackjack-blackjack ties, on a double-deck game a blackjack will occur once every 21.68 hands. Therefore the player will win an extra 25 cents once per 21.68 hands, for a net profit of 0.9032 cents per hand (less than a penny). The player’s net profit will be 90.32 cents per 100 hands because of this rule.
On a $5 game, if the player wagers $5.50 per hand and is paid $8 on a blackjack ($7.50 on the $5 wager and $1 on the 50 cent wager), then as I showed above, the player will win an extra 90.32 cents per 100 hands. Assume a house edge of 0.50% on the base game. Then the house edge on the main game will cost the basic strategy player who is wagering a flat $5.50 per hand (100)x($5.50)x(0.005) = $2.75 per 100 hands. By refunding 90.32 cents, the player will lose a net $1.85 per 100 hands. This effectively reduces the house edge to 0.33%. In other words, the house still has the edge.
As for your insurance question, in this case the player’s cards don’t matter. The player is simply considering a bet that the dealer has a ten-valued card in the hole when he shows an Ace up. In this case, according to your question, casino policy pays $5.50 on a $2.50 insurance bet. This is the same as insurance paying 2.2-to-1. In this case, the house still has an edge on the insurance bet of 0.583% in a double-deck game. Taking insurance gives no advantage to the player.
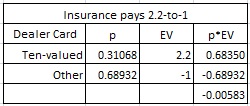
Neither of these situations allows the basic strategy player to gain an edge over the house and therefore would not be targeted by APs.


