The house rules for blackjack at most casinos allow players to "double for less." Simply put, a player can double a hand for an amount less than the amount of their initial wager. Doubling takes place when the player has a big advantage on a hand. In exchange for only receiving one more card, the player is allowed to increase his wager. Wagering anything less that the full double is equal to giving back some of the player's expected win amount. In short, it is dumb for a player to double for less, so the house is glad to allow players to do so.
On the other hand, it would be very unusual to find a casino that gives the player an opportunity to "split for less" (SFL). The standard split rule states that if the player is dealt a pair of identical cards (a pair), then the player can split them into two separate hands and receive a new second card on each, while being required to place a full initial bet alongside each split hand.
There are three reasons to split a pair. Some examples will help clarify these reasons. In the following examples, I am considering a standard six-deck shoe game (6D, H17, DOA, DAS):
1. To win more on a winning hand. For example, 9-9 vs. 6. For every $100 wagered, standing wins $22.03, splitting wins $45.29.
2. To turn a losing hand into a winning hand. For example, 8-8 vs. 6. For every $100 wagered, standing loses $12.46 and splitting wins $37.37.
3. To lose less on a losing hand. For example, 8-8 vs. T. For every $100 wagered, hitting loses $53.49 and splitting loses $47.51.
To understand why it can be advantageous to the player if he is allowed to SFL, consider the hand where the player holds 3-3 against a dealer 9. Here are the numbers for standing, hitting and splitting.
Holding 3-3 vs. 9:
• Standing on 3-3 vs. 9 loses $54.19 for every $100 wagered.
• Hitting on 3-3 vs. 9 loses $29.47 for every $100 wagered.
• Splitting on 3-3 vs. 9 loses $43.12 for every $100 wagered.
Because hitting loses the least amount it is the basic strategy play in this situation.
Now, consider if this player is allowed to SFL with his 3-3 vs. 9. The player leaves his original $100 wager on one of the 3 vs. 9 hands, but he only places a $5 wager on the other 3 vs. 9 hand. In this case the player's long-term loss rate is roughly $22.64 on the hand.
In other words, the player lost less than the $29.47 amount that basic strategy (hitting) would lose. It is better for the player to SFL than to follow basic strategy. In the best possible universe, the player should fully SFL (split for free). That is, he could simply split his 3-3 vs. 9 into two hands and wager $0 on the split hand. If the player could do this, he would only lose roughly $21.56 for every $100 wagered. This is exactly the same as magically turning his 3-3 vs. 9 into a 3 vs. 9, with a second card to come.
In other words, the extreme case of a SFL strategy is the same as discarding one of the starting cards in the split. The starting hand 8-8 vs. T becomes a much improved 8 vs. T (with a second card to come). The weak starting hand 9-9 vs. A turns into a substantially better starting hand 9 vs. A (with a second card to come). That's the magic of a being able to SFL.
But don't expect to go into your local casino and SFL. That isn't going to happen if management has the slightest clue about how to run their games. Casino management may not fully understand the mathematics of why players aren't allowed to SFL, but they have been taught to never allow it. Nevertheless, SFL happens.
The silver bullet for the advantage player is finding a game that allows "back betting." What back betting means is that if a player wagers on a spot, then other players are allowed to wager "behind" that spot on the same hand. The player who made the main wager (the main player) controls the action for the hand and makes all of the strategic decisions. When the hand completes, all back bettors are paid according to the final result determined by the main player's strategy.
Back betting requires the main player to play his hand according to the house rules, including fully matching his splits. However, back betting allows an important exception. In the case of a split hand, the back bettor is not required to match his wager and play the split. Instead, the back bettor is allowed to let his wager ride on the original hand in the split without matching his wager on any secondary split hand(s).
With a SFL team, the main player makes a very small wager, often table minimum, on his spot. The back bettor makes a very large wager behind. The main player knows that it costs very little to misplay his hand if it makes the opportunity available for the back bettor to make a very profitable SFL play. The main player plays a modified split strategy that affords the greatest possible return to the back bettor.
The fact is that there are casinos and jurisdictions in the U.S. and internationally that allow back betting. For example, many California card rooms allow back betting, and SFL teams can take advantage of it in exactly this fashion.
In giving the full SFL strategy, there are three possible options for the main player and back bettor whenever they are dealt a pair. They can:
• E = split for equal. The main player splits. The back bettor matches his main wager on split hand(s). This takes place when the back bettor is trying to win more in a winning situation.
• L = split for less. The main player splits. The back better does not match his main wager on split hand(s). This takes place when the back bettor is trying to lose less in a losing situation.
• N = don't split. The main player does not split the hand.
Here is full SFL strategy (assuming a six-deck shoe game): 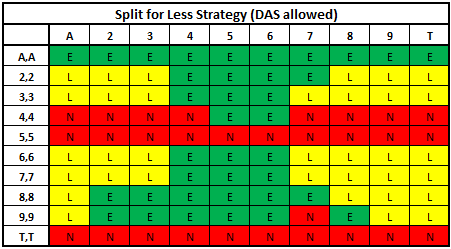
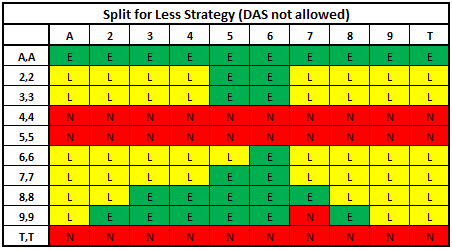
Obviously, the ability to SFL adds to the player-side of the house edge equation. Now for the bad news: not by that much. The situations where the player splits for less are uncommon. I calculate that full SFL strategy (split for free) adds about 0.16% to 0.20% to the player side (slightly more or less depending on the game rules). Unless the game starts with a very low house edge to begin with, the SFL player is not going to be able to turn the tables. However, such jurisdictions exist internationally, and there are active SFL teams engaged today in exploiting these games.
The strategy employed by the SFL team is not to beat the game of blackjack. Their advantage play methodology is to maximize benefits while playing a roughly even game. Their profit comes from exploiting all the other perks and cash incentives that come from being premium players in the casino. These incentives may include cash-back programs, room, food, beverage service, travel and airfare reimbursement, promotional chips, show up money, loss rebates and every other accommodation afforded to a premium player.
SFL teams try to minimize their exposure to the volatility of blackjack, while maximizing the apparent value of each player on their team. To do this they may also employ measures like skipping hands, slow play, rotating the big player role and deceptive betting to get rated higher than their actual averages.
A SFL team is not a substantial threat to the profitability of the table games department. Their target is marketing. These players are not engaged in a method of play that can beat blackjack outright. They are just interested in staying even, while exposing their team to as little risk as possible and getting rated as highly as possible. Their entire profit relies on exploiting and maximizing the various marketing incentives they receive by virtue of their high tier status.
A SFL team will play perfect basic strategy, with the exception of a few odd splits. Even careful observation of these teams may not quickly reveal their methodology. A reasonable game pace may yield only one or two deviant splits per hour. It takes alert and educated surveillance personnel and table games management to spot a team engaged in this obscure method of advantage play.


