In “Blackjack Attack, Playing the Pro’s Way, 2nd edition” (BA), author Donald Schlesinger presents the “World’s Greatest Blackjack Simulation.” One of his achievements was to determine the win-rate per 100 hands for six-deck blackjack, using the Illustrious 18 (see this post), and four additional indices, called the Fabulous 4 (used for late surrender decisions only). The purpose of the present article is to compare Schlesinger’s results with those obtained when I considered the World’s Greatest Blackjack Card Counter (see this post).
The simulation results I quote from BA have the following particulars:
- Six-deck shoe game, with the rules DOA and DAS.
- The counter uses the Illustrious 18 and Fabulous 4 (when the game permits late surrender), for a total of 22 High-Low indices.
- The counter does not play unless the count is in his favor (he “back-counts” the shoe).
- The counter does not compute the perfect true count based on the exact number of cards remaining. Instead, he computes the true count based on a human-feasible resolution of quarter-decks.
- The counter uses a 1-to-12 bet spread, increasing his bet with the count.
To better understand point #5, the counter’s base wager is called “1 unit,” which he plays with the lowest count at which he gets the edge (the lowest count at which he enters the game). Schlesinger then assumes the counter will raise his wagers as the true count increases, with a maximum wager of 12 units.
On page 197 of BA, Schlesinger presents the win-rate per 100 hands for a variety of rules and cut card placements. He expresses his results in terms of the number of units won per 100 hands. Schlesinger starts with the counter’s minimum bet and works up from there. To compare Schlesinger’s results to those I gave, we fix the counter's maximum bet of 12 units equal to $100, so that Schlesinger’s "unit" is $8.33. Schlesinger’s win-rate is then based on a maximum bet of $100. In other words, point #5 above becomes:
#5A. The counter spreads his bet from $8.33 to $100, increasing his bet with the count.
Schlesinger presents a real-world card counter. This counter uses either 18 or 22 indices (22 if late surrender is allowed), resolves the true count by quarter-decks, and spreads his bets 12-to-1, raising his bet with the count up to a maximum bet of $100. Here are Schlesinger’s results (LSR = late surrender):
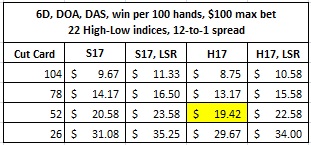
As I showed in this post, the perfect High-Low card counter with a maximum bet of $100, playing 6D, H17, DOA, DAS, with a cut card at 52 cards, has a win-rate of $33.58 per 100 hands. According to Schlesinger’s results, the player he modeled with a 12-to-1 bet spread has a win-rate of $19.42 per 100 hands (see highlighted yellow box). In other words, Schlesinger’s real-world model achieves 57.8% of the win-rate of the world’s greatest card counter. The average counter is giving up $14.16 per 100 hands in potential profit.
There is a weird way at looking at Schlesinger’s results that yields a higher win-rate under the assumption of a $100 maximum bet. If we fix the counter’s maximum bet at $100, then a smaller spread will yield a higher average wager and thus a higher win-rate. The narrowest spread that Schlesinger presented in BA is an 8-to-1 spread. To compare Schlesinger’s results for an 8-to-1 spread to those I gave, we fix his maximum bet of 8 units equal to $100, so that Schlesinger’s "unit" is $12.50. In other words, point 5 above becomes:
#5B. The counter spreads his bet from $12.50 to $100, increasing his bet with the count.
Here are Schlesinger’s results for this counter:
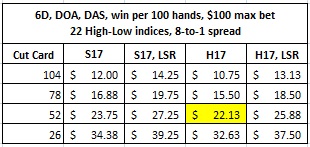
The perfect High-Low card counter with a maximum bet of $100, playing 6D, H17, DOA, DAS, with a cut card at 52 cards, has a win-rate of $33.58 per 100 hands. According to Schlesinger’s results, the player he modeled with an 8-to-1 spread has a win-rate of $22.13 per 100 hands (see highlighted yellow box). In other words, Schlesinger’s real-world model achieves 65.9% of the win-rate of the world’s greatest card counter. The average counter is giving up $11.45 per 100 hands in potential profit.
The world’s greatest card counter has a spread of 1-to-1, so that he either wagers $0 or $100; that’s the spread that maximizes win-rate. We see the effect of increased win-rate with decreased bet spread in the two comparisons presented above. The smaller the spread (with a fixed maximum bet), the more the counter wins.
Beginning on page 190 of BA, Schlesinger gives nine reasons that the counter may actually win less than the win-rates he presented. Here are some of his reasons:
- Using a weaker card counting system or fewer indices.
- Errors in computing the true count and other errors.
- Cover plays (e.g. not splitting 10’s) and other camouflage.
By fixing the maximum wager and working backwards, Schlesinger’s results show the true tale of woe for the average card counter.
I recall a day back in 2003 when I was card counting at the Golden Nugget in downtown Las Vegas. I was using a "play all" approach (not back-counting), with a minimum bet of $10 in neutral and negative counts, spreading to a maximum bet of two hands at $80 each. Suddenly, two players came up to the table and each placed a table maximum $500 wager. The true count was +2. I had met these two players before – they went by the Internet monikers OCKO and El Burro and were among the top players in Las Vegas at the time. After the hand was resolved (I don’t recall what happened), El Burro turned to me and said “we had the edge, of course we wagered the table maximum.” Sufficiently well-funded advantage players don’t care about camouflage, indices or bet spreads. They just make the bets.
A card counter walks in to your casino. You have a well-defended six-deck game with tight rules (H17, DOA, DAS) and cut card placed at 1.5 decks. You watch as this counter "Wong's" into the tables and spreads his bets from $10 to $100. You think, "Holy crap! Sound the alarms! We're getting crushed by this counter!" The truth? This counter is probably winning under $15 per 100 hands. Don't you have something better to do?


