The way baccarat usually operates, a winning Banker wager is charged a 5% commission, creating a house edge on the Banker bet of about 1.0579%. Another way of saying this is that a winning Banker wager pays 19-to-20. As commissions are collected and accounted, this challenging payout causes the game to slow down, losing profit for the house. One solution to this problem is to offer a "commission free" variation. These commission free versions work by choosing a rare winning Banker hand and not paying it full value. The two most common commission free variations (both public domain) are the following:
- Commission Free Variation #1: Banker winning three card seven is a push. House edge = 1.0183%.
- Commission Free Variation #2: Banker winning total of six. House edge = 1.4581%.
The first version has been known for a long time as EZ Baccarat. However, in 2013 the patent on this rule expired and other companies marketed the game under their own brands. In particular, Shuffle Master started pushing its Fortune 7 baccarat. Regardless, the big question is why any casino would want to offer a version of baccarat with a lower house edge than standard baccarat? By reducing the edge from 1.0579% to 1.0183%, the casino directly gives up profit. However, this profit is recouped in two ways. First, because the game is non-commission, it will move faster. Second, this version has a very popular side bet that almost always accompanies it on the table.
The side bet that accompanies variation #1 is most commonly known as the Dragon 7 bet (Shuffle Master branded it as the Fortune 7 side bet). The Dragon 7 pays 40-to-1 if the Banker hand is a winning three card 7, otherwise it loses. The Dragon 7 can be viewed as a type of insurance against the hand that creates the commission free structure. In other words, when the player wagers on Banker and gets a push based on the commission free rule, that same situation results in winning the Dragon 7. In combination with the main commission free structure, the Dragon 7 side bet is an extremely popular addition. It is this combination of bets that propelled EZ Baccarat to the top of the proprietary baccarat variant universe.
Unlike EZ Baccarat, variation #2 has been public domain since the beginning of casino-time. Moreover, it has a substantially higher house edge (1.4581%) than ordinary commission baccarat. It is a faster game with a higher house edge -- the best of both worlds. It follows that many baccarat-centric casinos internationally devote large parts of their gaming floor to this game rather than commission baccarat.
Given the "insure against the commission hand" theme of the Dragon 7 bet, it is natural to consider if there could be a similar side bet for commission free variation #2. Of course, the answer is yes.The Super Six (SS) baccarat side bet pays 15-to-1 if the Banker hand has a winning total of 6, otherwise it loses. The following table gives the combinatorial analysis for SS:
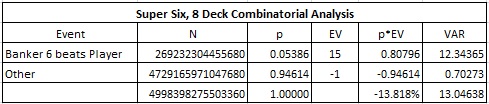
In particular:
- The house edge is 13.818%.
- The hit frequency is 5.386%.
- The standard deviation is 3.612.
There are a few easy observations to make.
- In order for a Banker 6 to beat the Player, the hand can't end in a natural. Like the Dragon 7, it's good when 8's and 9's leave the shoe.
- Obviously, a shoe rich in 6's is great for this bet.
- For the Banker to win with a total of 6 the Player hand MUST draw a third card (think about it). A great drawing card for the Player hand that will beat a Banker total of 6 is when the Player hand draws a 7. It is therefore good when 7's leave the shoe.
Putting this together, our intuition says that we don't like 7's, 8's or 9's in the shoe and we really like 6's in the shoe.
The following table gives the effect of removal for each card, together with a counting system corresponding to these EORs:
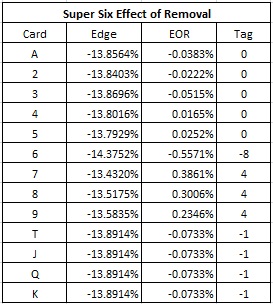
The recommended count system is:
- 6 = -8
- 7, 8, 9 = +4
- T, J, Q, K = -1
I note that this system has an excellentbetting correlation of 0.985. However, one should not be optimistic here at the prospects of a card counting bonanza. A 13.8% house edge is a lot to overcome.
With regard to the -1 tag, note that a 0-valued card absolutely will not help improve a Player hand on a draw to a total of six under any circumstance (Player draws with a total of five or less). This effect is small, but a shoe rich in 0-valued cards will move the edge towards the player.
I conducted a simulation of one hundred million (100,000,000) eight-deck shoes using the count system above, with the cut card placed 14 cards from the end and the usual burn card rules. The following table summarizes the baccarat card counting statistics for SS:
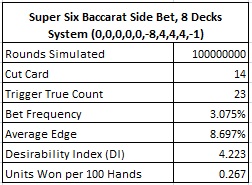
A desirability index (DI) of 4.2 puts this wager well into the "low risk" category.
The dedicated SS card counter (a person who almost certainly does not exist) may choose the following far easier but not nearly as efficient card counting system:
- 6 = -3
- 7,8,9 = +1
- Others = 0
This system has a much weaker betting correlation of 0.942. Nevertheless, its ease of use may trump its linear weakness.
I conducted a simulation of one hundred million (100,000,000) eight-deck shoes using the easier count system above, with the cut card placed 14 cards from the end and the usual burn card rules. The following table summarizes the card counting statistics for SS:
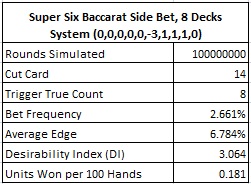
The win rate with this system goes down from 0.267 units per 100 hands to 0.181 units per 100 hands, a loss of nearly a third of the value. But there you go, if you're not going to count this side bet anyway, you might as well not do it with the best possible system.
My opinion is that the most desperate card counter may give counting this side bet a try. As usual, watch for players making the SS side bet late in the shoe at the table maximum, players table-hopping to make the SS bet (team), and players making multiple SS bets by wagering on other player's SS spots.


