When Don Johnson (DJ) beat several East Coast casinos in late 2011 through early 2012 by exploiting their loss rebate programs, few understood the scope of his triumph. After his success, there were a number of articles (for example, this article in Atlantic Magazine) that tried to explain his success as a mix of luck and experience. Several other articles produced mathematical analyses that did not directly address the main questions. As I described in this post, DJ succeeded because there was an off-the-top profit to be made simply by playing within the constraints he negotiated and strategically choosing quit points. The question I pose in this post is if DJ could have done even better?
At the World Game Protection Conference in 2013, DJ gave a keynote address in which he discussed his triumph. In it, he stated that there were three constraints placed on his play.
- He had to place one million ($1,000,000) dollars cash in the cage.
- He was allowed to wager a maximum of $100,000 per hand.
- If he lost $500,000 or more in a day, he could stop playing and get a 20% rebate on the totality of his losses for the day.
The common wisdom in the aftermath of DJ’s success was that DJ should play until he either lost or won $500,000, then quit for the day. As I showed in my previous post, this “wisdom” about optimal stopping points is patently false. With a one million dollar starting bankroll, DJ’s optimal quit points were to stop when his current bankroll was either less than $200,000 (quit-loss) or after winning $2,000,000 (quit-win).
With these stopping points:
- DJ’s average edge over the house was 0.63%.
- DJ’s expected total win per day was $85,800.
- DJ’s expected number of hands per day was 137.
Yesterday, I realized that there was a hidden assumption in my analysis: that Don Johnson must deposit exactly $1,000,000, no more, no less. As I researched this assumption online, I could find no evidence in any of the multitude of media articles about DJ that he ever deposited more than $1,000,000. Did he? I don’t know. Regardless, the question is if he could have won even more by strategically sizing his deposits to reflect specific market conditions.
To be precise, suppose that in addition to the two strategic decisions (quit-win, quit-loss) DJ could make about when to stop for the day, there was a third decision he could make as well: the size of his starting bankroll. What if the requirement for DJ was not that he place exactly one million dollars in the cage, but instead the requirement was that DJ place at least one million dollars in the cage? Was his deposit amount a variable under his control? Could DJ have made even more by depositing an optimal amount in the cage?
Here is the setup for DJ’s optimization problem:
- DJ’s starting bankroll per day was at least $1,000,000.
- DJ was allowed to wager $100,000 per hand.
- DJ was given a 20% rebate on his full losses if he lost at least $500,000 in a day.
Given these constraints, what are the appropriate bankroll, quit-loss and quit-win points to maximize DJ’s daily net income?
To answer this question, I ran a bunch of simulations. I simulated starting bankrolls from $1,000,000 to $5,000,000 (incremented by $250,000). For each starting bankroll in this range, I determined DJ’s optimal quitting points by simulating DJ’s net win for a range of different quit-win and quit-loss points and choosing the quit values that gave the maximum net win. The net win for each triple (bankroll, quit-win, quit-loss) was determined by conducting a simulation of ten million (10,000,000) “Don Johnsons” with those parameters and then averaging those results.
The following table gives the details of these simulations. For each bankroll, this table gives DJ’s optimal quit-win point. Stopping at this quit-win value maximizes DJ’s expected net win for the day. The quit-loss points are not given. The correct answer for quit-loss is to quit whenever there are fewer than two bets remaining (less than $200,000) in the bankroll.
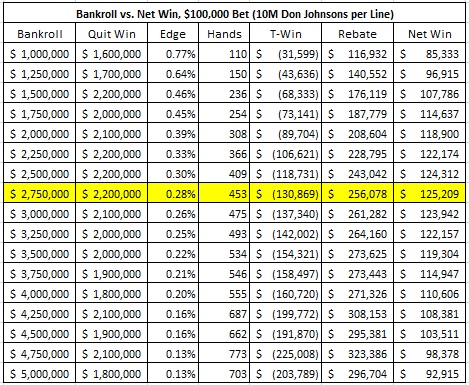
Note that these values were arrived at by simulation; they are not exact. Because of this, the values are subject to the natural volatility of the game. For example, in the results above, DJ’s expected net win per day was $85,333 with a $1,000,000 starting bankroll. In this previous article, I found that DJ’s expected net win per day was $85,800 with a $1,000,000 starting bankroll. Simulations are rough justice, at best.
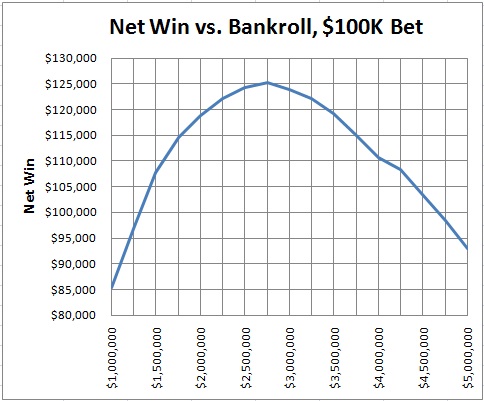
The following graph is based on the previous table. It presents DJ’s average daily net win versus his daily starting bankroll. The image clearly shows that DJ’s starting bankroll plays a strong part in maximizing his earnings:
Considering the data in the table and graph given above, here is DJ’s optimal strategy for maximizing his expected daily net win:
- Place $2,750,000 in the cage every day.
- Quit after winning $2,200,000 (bankroll = $4,950,000).
- Quit after losing more than $2,550,000 (bankroll < $200,000).
In this case:
- The average edge over the house is 0.28%.
- The expected total win per day is $125,209.
- The expected number of hands per day is 453.
To put it simply, playing with a starting daily bankroll of $2,750,000 instead of $1,000,000 would have given DJ approximately 46.7% more in expected daily net win.
Not every casino allowed DJ to make a $100,000 bet. He indicated that in some of his play, his bet was limited to $50,000. I repeated the analysis and simulations above with this constraint. In other words, I also found a solution through simulation to the following optimization problem:
- DJ’s starting bankroll must be at least $1,000,000.
- DJ was allowed to wager $50,000 per hand.
- DJ was given a 20% rebate on his full losses if he lost at least $500,000 in a day.
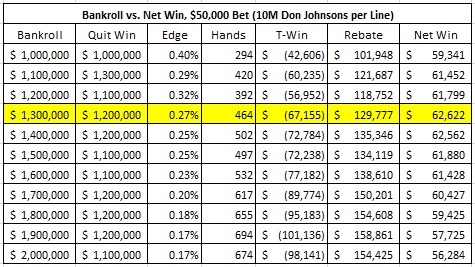
The following table gives the details of these simulations. For each bankroll, this table gives DJ’s optimal quit-win point. Stopping at this quit-win value maximizes DJ’s expected net win for the day. The quit-loss points are not given. The correct answer for quit-loss is to quit whenever there are fewer than two bets remaining (less than $100,000) in the bankroll.
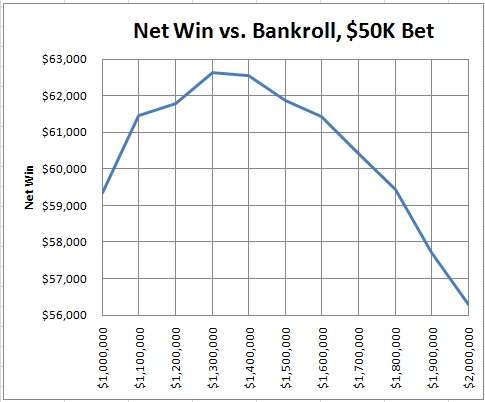
The following graph presents DJ’s average daily net win versus his daily starting bankroll, in the case when his maximum bet is $50,000:
Considering this data, here is DJ’s optimal strategy for maximizing his daily net win:
- Place $1,300,000 in the cage every day.
- Quit after winning $1,200,000 (bankroll = $2,500,000).
- Quit after losing more than $1,200,000 (bankroll < $100,000).
In this case:
- The average edge over the house is 0.27%.
- The expected total win per day is $62,622
- The expected number of hands per day is 464.
By playing with a starting daily bankroll of $1,300,000 instead of $1,000,000, DJ would gain 5.5% more daily net win. This is not much of a gain, but the principle remains the same.
When coming up with any advantage play strategy, the first step is to realize those variables that are under control and those that are not. For example, a blackjack card counter cannot control the number of decks being used, but he may be able to negotiate the penetration between shuffles. A hole-card player can’t change the dealing procedure, but he can use that procedure to create circumstances where the hole-card is more likely to be flashed. The edge sorter can’t change the cards, but he can engage in social engineering to get vulnerable cards sorted.
I have never heard of a casino that would limit a premium player’s deposit to 10 or 20 bets. If DJ did not deposit more than $1,000,000, then he sacrificed significant profit by not taking advantage of one of the variables under his control.


