Casinos use loss rebates as an incentive to draw high-limit play. The player who wins gets to keep 100% of his winnings. The losing player is given back a certain percentage of his losses as a direct cash rebate. Typical rebates range from 5% up to 20%, depending on the player’s bankroll and average bet. Loss rebates originated as a way to get players to quickly pay off a line of credit, but in recent years have become an expected perk of high-limit play. Many casinos now offer loss rebates on the big four: baccarat, blackjack, craps and roulette. The possibility of advantage play against these rebates has recently become common knowledge, thanks to Don Johnson (see this blog article) who brought this vulnerability to light in dramatic fashion in early 2012.
In order to safeguard these rebates from abuse it is necessary to require a certain number of hours of play to be eligible for the rebate. This insures that the casino will earn sufficient theoretical win (T-Win) to overcome the cost of the rebate. In absence of a time requirement, a minimum loss requirement is sometimes used instead. Don Johnson showed that loss rebates on blackjack, when based on a minimum-loss criteria, are highly vulnerable to advantage play. This article considers loss-rebate advantage play against roulette.
In proceeding theoretically, I am not going to place a time-requirement or loss-requirement on the player in order to be eligible for a loss rebate. Instead, I am going to assume the player has the best possible circumstances; he can quit playing at any time. If the player wins, he keeps 100% of his winnings. If the player loses, he gets an unconditional loss rebate of the proscribed percentage.
The rebates I am going to consider have percentages 10%, 12%, 15%, 18% and 20%. The only constraints on this player are his win/loss stopping points. These points are a loss-exit-point and a win-exit-point. The player stops playing after having lost a certain amount or after having won a certain amount. The “time” stopping point will not be considered. That is, we will assume that the player continues to play until he hits either the win or loss threshold, no matter how short or long it takes. For a given rebate percentage, there are optimal stopping points that maximize the player’s theoretical return.
I am going to assume a high-limit player is playing single-0 roulette, with a table maximum of $1000 straight-up on any number. This is a common table limit that I have seen in high-limit rooms. Given this table limit, one of the most common wagers for the high-limit player is called a “complete bet.” When making a complete bet, the player is wagering all ways to a given number on the inside (see this article at Wikipedia).
For example, a complete bet on 17 is equivalent to the following wagers:
- $2,000 on 13, 15, 19, 21
- $4,000 on 14, 20
- $6,000 on 16, 18
- $12,000 on 17
This allows the high-limit player to wager $40,000 on the inside on a table with a $1000 maximum. If a player makes a complete bet on 17, and 17 hits, then the player wins $392,000.
To determine the optimal stopping points, I ran a lot of simulations. For each rebate percentage, and for each type of bet (straight-up and complete) I ran several hundred combinations of possible win-exit-points and loss-exit-points. For each combination of exit points, I ran ten million (10,000,000) simulated high-limit players. I then averaged together the results for these ten million players to get the average result for a player with the given exit points. By virtue of these simulations, the program “converged” to the best possible exit points. In this way, I determined the specific win/loss exit-points that optimize the average net win for the player.
In presenting my results about loss rebate advantage play on single-0 roulette, I need some definitions:
- Rebate Percent. This is the percentage of losses the player will be refunded if he stops playing with a loss.
- Loss Exit Point. The player should stop playing and collect his rebate when he loses this amount (or more).
- Win Exit Point. The player should stop playing when he wins this amount (or more).
- Average Rounds. Players will play different numbers of rounds with the given stopping points. This value is the average length of play with the given stopping points.
- Average Theoretical win (T-Win). T-Win is defined to be (total wagers) x (house edge). In considering the ten million simulated players, there was a distribution of T-Wins among these players. This value represents their average. It is simply (Average Rounds) x (1/37).
- Average Rebate. Among the ten million players, some won and some lost. Those who won did not get a rebate. Those who lost, got a rebate according to the given rebate percentage. The value in this column gives the average of these rebates.
- Average Net Win for Casino. By definition, this number is simply (Average T-Win) – (Average Rebate). The fact that these numbers are negative indicates that the player has a positive expected value playing against the rebate. In other words, this is an advantage play.
- Rebate as % of T-Win. This number is (Average Rebate)/(Average T-Win). In evaluating the value of a discount to the player, it is common to determine the percentage of T-Win being returned. Any percentage higher than 100% indicates a player edge.
The following table summarizes my analysis of loss rebate advantage play for a player who is making a $1000 straight-up bet:
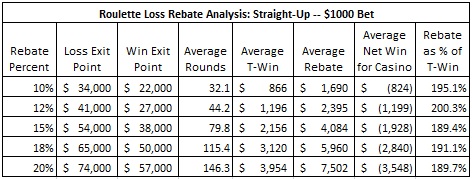
Given the limitation on the wager ($1000), it is unlikely that a highly funded team would attack roulette in this way. Complete bets are a different story.
The following table summarizes my analysis of loss rebate advantage play for a player who is making a $40,000 complete bet:
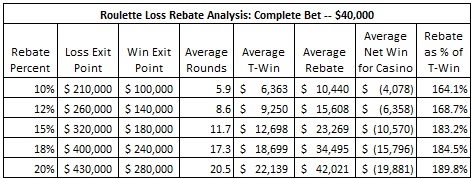
Note the extremely short average playing time for the advantage player who is making a complete bet. Given that roulette typically moves at a pace of about 30-to-40 rounds per hour, the “average rounds” indicates play time well under one hour on average. In other words, optimal advantage play will be hit-and-run.
By making complete bets to exploit loss rebates, the AP will have expected winnings up to $20,000 for less than one hour of work. These are the kind of numbers that will draw in the best and most well-funded advantage player teams.
There are a number of ways to protect roulette from loss-rebate style advantage play:
- Watch for players who play hit-and-run style.
- Watch for players who leave after small wins, but continue playing through larger losses.
- Evaluate all players who are making complete bets at the table maximum.
The best safeguards are, unfortunately, also the most challenging to implement
- Do not give loss rebate discounts for roulette. Instead, give a fixed “percentage of T-Win” rebate, similar to what is done on slots.
- Change the discount policy to require a minimum playing time (number of rounds) to be eligible for a loss rebate.


