I created an Excel spread sheet that computes the optimal stopping point for a loss rebate advantage play opportunity using the Loss Rebate Theorem (LRT). You can download it free of charge (and at your own risk) by clicking here:
Loss Rebate Theorem Excel Spread Sheet
Based on the recent Revel loss rebate promotion, the default settings are for 9/6 Double Double Bonus video poker, with an 800 unit bankroll, a 100% loss rebate and a wager size of $125. The house edge is -1.019217% and the standard deviation is 6.479582.
Here is an image of the default set up. The user inputs values in the green areas. The spread sheet completes itself from there:
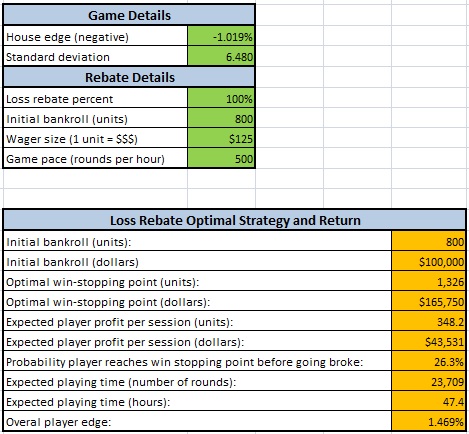
Here are the details:
- The player is assumed to play until he loses his entire bankroll or his current bankroll equals or exceeds the win-stopping point.
- The player has no "time threshold." He keeps playing until he hits a bankroll stop point.
- This spread sheet will fail if the optimal win-stopping point is more than 10,000 units above the number of units in the bankroll.
- If no advantage play is possible, the spread sheet will indicate this with a warning message.
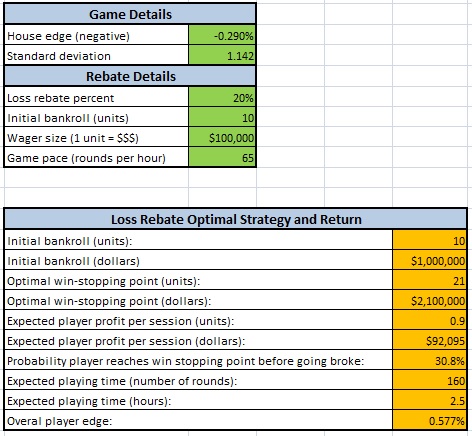
If you want to see the LRT behave badly, try using it on video poker with a small bankroll. Then, to see how accurate it can be in good conditions, try the spread sheet using the parameters that Don Johnson negotiated:
- House edge = -0.00290361 (-0.290361%)
- Standard deviation = 1.1417
- Loss rebate percent = 20%
- Wager size = $100,000
(House edge and standard deviation from Appendix 4 at wizardofodds)
When Don Johnson played, he was required to put at least $1M in the cage. With $100k wagers, his bankroll was only 10 units. This image shows the results of the LRT for a 10 unit bankroll for the game Don Johnson played: