And I am dumb to tell the crooked rose
My youth is bent by the same wintry fever.
-- Dylan Thomas
Casino War (CW) is based on the children’s card game War in which one player attempts to win all the cards from the other player. In its casino form, it is extremely easy to play, with essentially no decision-making. This makes it a frequent choice for new table games players, but CW rarely attracts more seasoned players. The reason for this article is that I got an e-mail from a surveillance manager in an overseas casino who wrote that he was very concerned that his CW was being edge sorted (see this post). He asked me to analyze edge sorting CW for him. Oddly, the possibility of edge sorting CW never before occurred to me. In retrospect, this post is long overdue.
CW is usually dealt from a One2Six continuous shuffler (see the picture below) where the players are not allowed to touch their own cards. Note that the next card to be dealt is clearly visible before it is dealt. In particular, if the cards inside the One2Six have been edge sorted, the bottom edge of the next card to be dealt can easily be distinguished.

Here is a picture of a CW table using the One2Six shuffler (image found on Google images). Note the brush shield that covers the next card to be dealt:

Like baccarat, it is hard to imagine how the cards inside the One2Six could be edge sorted. Maybe a crazy high-roller can convince the casino to turn certain cards. It is possible that at some casinos the players are allowed to touch their cards. Maybe there are issues with the shuffler itself that can be exploited. Maybe there is collusion with management. Regardless, if cards can be identified, the edge that is possible is extraordinary.
As a reminder, here are the most common rules for CW:
- After making a wager, the dealer and player each receive a card face up. If the player’s card is higher in rank than the dealer’s card, the player wins even money. If his card is lower, he loses his wager. Ace is high.
- If the player’s card matches the dealer’s in rank, the player can surrender and recoup half his bet, or he can go to war (basic strategy is to always go to war).
- When going to war, the player places an additional war wager equal to his original wager. The player and the dealer each get another card. If the player beats the dealer, he wins even money on his original wager and his war wager is a push. If he ties the dealer, he wins even money on both his original wager and war wager. If the dealer beats the player, the player loses both his original wager and war wager.
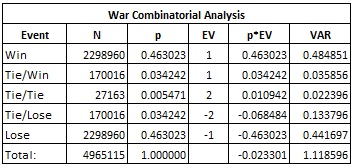
The following table gives the combinatorial analysis for CW:
In particular:
- The house edge is 2.3301%.
- The standard deviation is 1.0576.
- The win frequency is 50.2735%.
Note that the player wins more than 50% of his hands. This may be part of the reason that CW survives as a casino game. The house edge arises because the player wins one unit in the case Tie/Win, but loses two units in the symmetric case Tie/Lose.
In CW, the first card usually goes to the player seated at first base. If the cards have been sorted and this player can observe the top of the first card, then this is the seat that will have information about a card to be dealt in the next round.
The following table gives a breakdown of the edge by the rank of the first card dealt to the player:
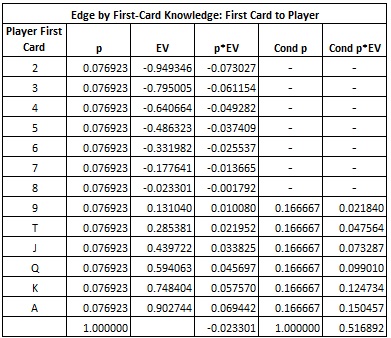
The player has the edge if the card he receives is 9, T, J, Q, K or A. Otherwise, the house has the edge. It follows that the player should sort the cards into these two groups:
- Group #1 = {2, 3, 4, 5, 6, 7, 8}
- Group #2 = {9, T, J, Q, K, A}
The AP’s strategy is to make a large wager whenever the card he will receive belongs to Group #2, otherwise he will either make a small wager or sit out the hand. Here are the summary statistics for edge sorting CW:
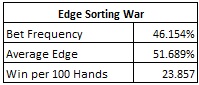
An average edge of 51.689% is extraordinary for the AP. Even at a $100 wager, edge sorting yields over $2300 profit per 100 hands. If an AP can identify the Aces and Kings and no other cards then he can earn over $1270 in profit per 100 hands with $100 wagers. In CW, any card knowledge gives the AP a powerful advantage. There is little doubt that if a card identification opportunity exists for CW at a casino, the game will be targeted.
Dealing procedure at some casinos has the dealer receiving the first card out of the continuous shuffle machine. The following table gives a breakdown of the house edge by the rank of the first card dealt to the dealer:
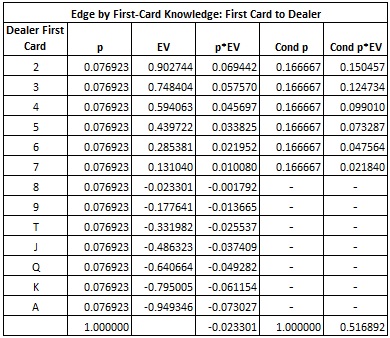
The player has the edge if the card the dealer receives is 2, 3, 4, 5, 6 or 7. Otherwise, the house has the edge. It follows that the player should sort the cards into these two groups:
- Group #1 = {8, 9, T, J, Q, K, A}
- Group #2 = (2, 3, 4, 5, 6, 7}
The AP’s strategy is to make a large wager whenever the card the dealer will receive belongs to Group #2, otherwise he will either make a small wager or sit out the hand. If the first card is dealt to the dealer then this provides an AP team with a substantially greater opportunity: every seat can take advantage of the information.
Casino War is extremely vulnerable to any system that allows individual cards or groups of cards to be identified. Including a “turn” as part of the shuffle procedure is the usual remedy against edge sorting. Because the shoe is never fully shuffled when using a CSM, a “turn” is not possible. There is another easy fix.
Note that the ability to use edge sorting or other card identification method against CW requires a clear view of the top card before it is dealt. I recommend the following:
- The first card to come out of the shuffler should be burned each round.
I will add that there are other card identification methods that have been used against the One2Six. These methods are beyond the scope of this blog.


