In many casinos, cash wagers are not permitted for table games. Instead, the circle of life is to give the casino some cash, get chips, play for a while, win or lose some chips, and finally exchange the chips in your possession for cash at the cashier’s cage. Or, as a friend of mine would say to the pit boss, with her cute deer-caught-in-the-headlights look: “you mean I can actually get cash for these things, I never did that before?”
In many casinos, cash wagers are not permitted for table games. Instead, the circle of life is to give the casino some cash, get chips, play for a while, win or lose some chips, and finally exchange the chips in your possession for cash at the cashier’s cage. Or, as a friend of mine would say to the pit boss, with her cute deer-caught-in-the-headlights look: “you mean I can actually get cash for these things, I never did that before?”
When a player puts his money on the felt in exchange for chips, that money is placed into a metal box next to the casino table. The cash that goes in doesn’t come out until much later when it is counted. The total money at the table that is exchanged for chips is called the “drop” for that game. If more than one table of a game is offered, the drops are often totaled together to get an overall drop for that game in the casino. Casinos rarely consider drop for a single player. Instead, the drop is totaled overall players of a game (or all players for all tables of a game), for a shift, a day, a week, a month, a quarter, or a year.
The “win” is the amount the casino won on that game. This amount is from the casino’s point of view, not the player’s. So, if a player exchanged $500 in cash for chips at roulette, and left the table with $325, then the win is $175. If the player exchanged $500 in cash and left with $850, then the win is -$350. A negative win means the casino lost and the player won.
As with the drop, casinos rarely consider win for a single client. The win is totaled overall players of a game (or all players for all tables of a game), for a shift, a day, a week, a month, a quarter or a year.
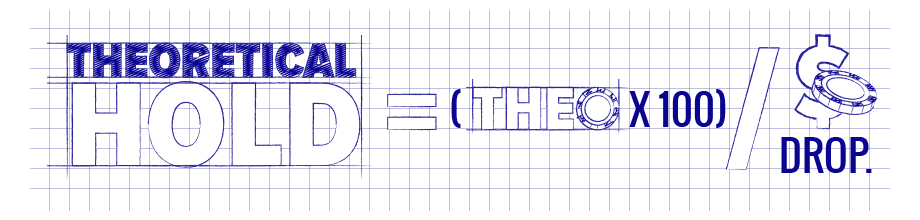
Finally, the “hold” is defined to be a percentage, and is given by the equation:

For example, if a casino dropped $54,000 at roulette for a week, and won $8,800 during that same week, then the hold for the week is:

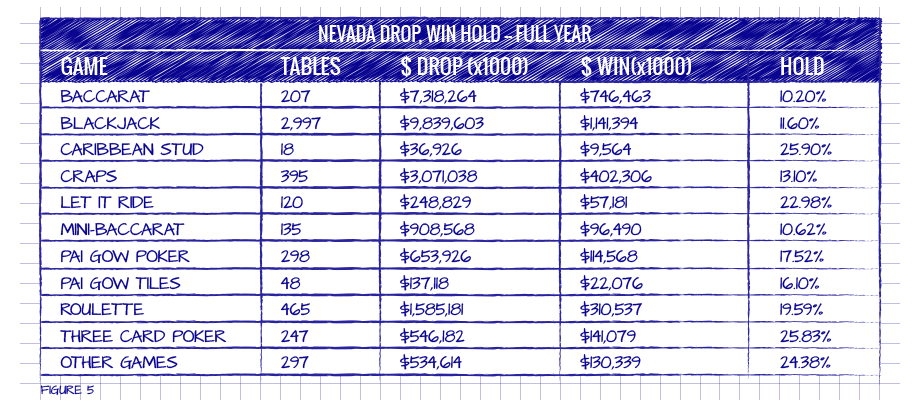
Figure 5 gives the Nevada statewide drop, win and hold statistics for the fiscal year July 1, 2008 to June 30, 2009. For example, blackjack dropped $9,839,603,000. The casino win was $1,141,394,000. The hold was:
Hold = ($9,839,603,000 ×100) / $1,141,394,000 = 11.60%.

Drop indicates how much activity is happening at the table. The higher the drop, the more players are handing money to the dealer and asking for chips. Having a high drop is a good thing; it indicates player interest. Of course, having a high win is also good; the casino wants to make as much as possible from each game.
The higher the win, the more the casino is earning from actual gameplay. The tenuous balance between the desire to have both a high drop and a high win is measured by the hold. So, the first lesson about the hold is that there is no theoretical hold percentage for a game that can be computed. More precisely, it is defined to be a ratio of two quantities, neither one of which can be theoretically computed.
If the win gets too high compared to the drop, then people won’t want to play, so the drop will get smaller as people move away from the game. As a result, the hold is likely to be a larger percentage. A game with a hold over 30% is usually winning too much too fast and burning out players. Conversely, if the win is too low, then people will flock to the game because it will be viewed as loose. It is likely to have a higher drop, and hence the hold is likely to be a smaller percentage. A game with a hold under 10% is winning too little too slowly and the situation will become intolerable to the casino. A reasonable hold for a casino game is between 10% and 30%, which is what Figure 5 indicates.
Hold is measured by examining the dollar value amounts computed by the normal accounting procedures used in table games. It is also possible to compute the theoretical hold, which is defined by the following equation: