RTP (RETURN TO PLAYER)

The “Return to Player” or RTP for a casino game is defined by:

Note that this number is based on actual wagers and actual winnings. It is not a theoretical number. It is not computed by a spread sheet computation, by running a cycle, or by extensive game simulation. The RTP is based on real people placing wagers on games in a live casino environment.

For games that have no strategy (like Casino War, craps or roulette) it is usually the case that:

Moreover, the greater the number of times the game is played, the more the RTP represents information about the actual return of the game and the more “exact” we expect this equation to become. “Exact” does not mean that the two sides get closer and closer to each other. What it does mean is that the ratio of the two sides of this equation gets closer and closer to 1 as the number of rounds gets larger and larger. [100% – (House Edge)] / RTP > 1

The number 100% – (House Edge) is referred to as the game’s theoretical RTP. Sometimes the language gets loose here, and the value 100% – (House Edge) is referred to as the game’s RTP.

LET’S LOOK SOME EXAMPLES:

For roulette, the RTP is 100% - 5.26% = 94.74%
Consider a player who is shooting craps and betting the pass line with no odds for a house edge of 1.41%. Because there is no strategy in craps, the RTP for the pass line bet is 100% - 1.41% = 98.59%. For Jacks or Better with the “9/6” pay table, the RTP is 100% = 0.46% = 99.54%. With the “8/5” pay table, the RTP is 100% - 2.70% = 97.30%.

Loose slots have a RTP above 96%. Tight slots have a RTP below 92%.
Let's go back to those lotteries and investigate the RTP. In each lottery there were 1 million tickets. Let's assume that each of those 1 million tickets was purchased. The total amount wagered by the players is $1,000,000. The total amount won by the players is $900,000: either 900,000 tickets that paid $1 each or 9 tickets that paid $100,000 each. Thus the RTP if we run a full cycle is:

Assume we offer lottery 2 and sell 500,000 tickets. Thus, the total amount wagered is $500,000. We know that exactly 90% of the tickets are winning tickets. So, based on knowing the house edge, we expect the players to win approximately 90% of $500,000, or about $450,000. The state has a theoretical win of $50,000 to purchase shoes for the kids. For lottery 2, this income is pretty certain because of the high hit frequency (hit frequency = 90%) and the low payout of the winning tickets. The theoretical RTP of 90% transfers to a fairly accurate expectation about the real world.

Now, assume we offer lottery 1 and sell 500,000 tickets. Again, the total amount wagered is $500,000. There are only 9 winning tickets in the lot of 1 million tickets, so somewhere between 0 and 9 of the winning tickets will be sold. It is most likely that either 4 or 5 winning tickets were sold. Slightly less likely is that either 3 or 6 winning tickets were sold. And so on, with the most improbable case being that either 0 or 9 winning tickets were sold.

Based on the house edge of 10%, we expect the players to win approximately 90% of $500,000 or $450,000. Because the winning tickets are each worth $100,000 and there are only 9 winning tickets, the players actually won some unknown hundreds of thousands of dollars, from $0 to $900,000. The most likely case will be that the players won either $400,000 or $500,000 (4 or 5 winning tickets). There is simply no way to win 90% of $500,000 ($450,000). If we sold 4 winning tickets, the RTP is ($400,000) / ($500,000) = 80%. If we sold 5 winning tickets, the RTP is ($500,000) / ($500,000) = 100%. We can never have an RTP of 90% if we sell exactly 500,000 tickets.

We now consider some actual casino examples. If the player shoots one million rounds of craps betting the pass line, and he wagers $1 on each round, then at the end of those one million rounds the player has wagered $1,000,000. The player has "theoretically" won back somewhere in the neighborhood of $985,900 of those wagers. Because winning and losing on the pass line happen about equally as often (like lottery 2), it's a safe bet that the player's actual win and theoretical win are going to be pretty close, so the RTP should be pretty close to 98.59%. The more the game is played, the closer the RTP will get to 98.59% on the pass line.

Suppose a player is playing roulette and is betting $1 straight up on red-7. In this situation, the house edge is 5.26%. Therefore we expect the RTP to be approximately 94.74%. If this player bets $1 on red-7 on one million spins of the roulette wheel then at the end of those spins the player has wagered $1,000,000 and has "theoretically" won back approximately $947,400. Because hitting red-7 is an event that doesn't happen very often (1-in-38), it is reasonable to expect the player's actual win and theoretical win are substantially different (like lottery 1). Now suppose a player wagers that same $1,000,000 one wager at a time on “even” instead of red-7. In this case, because winning and losing happen about equally often, the RTP will quickly converge to 94.74% for this player.

The point is that the theoretical RTP should be pretty to the actual RTP for games that require no strategy and have a high hit frequency. The more rare a winning event (the lower the hit frequency), the more play is required for these values to converge to each other.

For games that have a strategy, mistakes will be made by the players. Because of this, the value of the RTP is usually less than 100% – (House Edge). For games with relatively trivial strategy (like Three Card Poker), the RTP is usually only slightly less than 100% – (House Edge). For extremely complicated games, like Blackjack Switch or Super Fun 21, the RTP can be several percentage points below the theoretical value.

Many casinos (especially online casinos where every player interaction is logged) create monthly RTP reports so they can track the exact performance of each game. Figure 4 gives examples of some RTPs for a month from an online casino based on live play. Looking carefully at this table, we can make some observations.

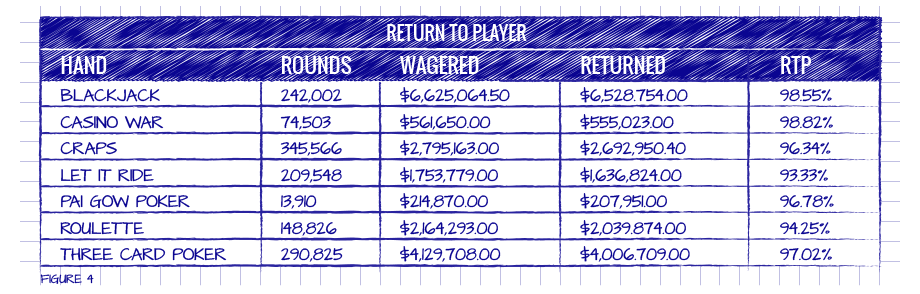
Note that blackjack, Let it Ride, Pai Gow and Three Card Poker are all returning below the theoretical RTP for perfect strategy. Based on the results given in Figure 1, blackjack has a theoretical RTP of 99.54%, Let it Ride has a theoretical RTP of 96.49%, Pai Gow Poker has a theoretical RTP of 97.34%, an Three Card Poker has a theoretical RTP of 97.15%. On the other hand, Casino War is above the theoretical RTP of 97.10% and roulette is close to the theoretical RTP of 94.74%. The RTP for craps cannot be analyzed because of the variety of wagers available.

Be careful of a common fallacy here. The cards, dice, reels and wheels don’t know what theoretical RTP they are supposed to be and try and get there. If the RTP is 94.25% at Roulette after 148,826 spins, there is no expectation that the game will try and make that up in the next 148,826 spins, so that the RTP moves closer to the theoretical value of 94.74%. If the pass line in craps is returning 102%, that does not mean the dice are due to go cold. The actual RTP is not an indication of what’s bound to happen in the future to make up the difference. Or, as they say in mutual funds and other investments, past performance is not an indicator of expected future performance.