Double Draw Poker (DDP) is a relatively new game that appears to be gaining ground in some markets, both in the US and internationally. The first time I saw DDP was at the Global Gaming Expo in 2013. After learning how DDP was played, I immediately commented to the game developer that DDP appeared to be extraordinarily vulnerable to collusion (information sharing among players). Over this last week, I finally did the work to quantify this vulnerability. The edge the advantage player can gain over DDP rivals hole-carding Mississippi Stud (see this post and this post). DDP collusion is in the stratosphere of advantage play opportunities against proprietary games. For the AP who is looking for the greatest new thing out there in proprietary games, DDP collusion must surely be near the top of his list.
DDP is played with a 54-card deck consisting of the normal 52 cards plus two Jokers. These Jokers are semi-wild, like Jokers in Pai Gow Poker. These Jokers can only be used to complete straights and flushes. Otherwise, they count as an Ace. DDP is not a game where the player competes against the house. Rather, the player competes against a pay table.
The play of DDP is easy to outline (I give the full details below). Play begins with the player being dealt a five-card poker hand. The player can then either fold or play. If he plays, he can discard and draw either 0, 1, 2 or 3 cards. The player can then once again either fold or play. If he plays, he can discard and draw 0 or 1 cards. The player’s final hand determines his result. He needs a final hand of two-pair or better to win.
The reason that collusion works should now be obvious. If six players are seated around the table, the players will collectively know at least 30 out of the 54 cards when making their first draw decision. If these six players share information about their hands, their draws will become substantially more accurate. Moreover, the player seated at third base may know up to 45 cards before he makes his first draw. This happens if each of the five players before him draws 3 cards. Imagine drawing to a poker hand knowing all but nine cards.
Sharing full information among six players and subsequently playing perfect draw strategy is not a human-feasible method of advantage play. But, the edge the players have over the house is large enough that there is plenty of room to simplify communication and draw strategies, while still achieving a substantial edge. I have not attempted to quantify such strategies, nor do I anticipate doing so. For me, it is enough to show what is possible.
Here are the rules in more detail:
-
The player begins by making an Ante wager and a Bonus wager of equal amounts. The player then receives five cards.
-
After viewing his cards, the player can fold or play.
-
If the player folds, he forfeits his Ante and Bonus wagers.
-
If the player plays, he must make an additional wager equal to his Ante wager (his first Draw wager).
-
The player can then play his current hand, or he can draw 1, 2 or 3 cards to try to improve his hand.
-
If the player draws, then the dealer deals the player new cards to replace his discards.
-
After the first Draw, the player can once again fold or play.
-
If the player folds, he forfeits his Ante, Bonus and first Draw wager.
-
If the player plays, he must make an additional wager equal to his Ante wager (his second Draw wager).
-
The player can then play his current hand, or he can draw 1 card to try to improve his hand.
-
If the player draws, then the dealer deals the player 1 card to replace his discard.
-
If the player’s final hand has poker value two-pair or better, then the player wins, as described below. Otherwise the player loses and forfeits all wagers.
If the player’s final hand has poker value two-pair or better, then the player is paid even money on his Ante and Draw wagers. His Bonus wager is paid according to the following pay table:
-
Five of a Kind pays 500-to-1
-
Natural Royal Flush pays 100-to-1
-
Wild Royal Flush pays 50-to-1
-
Straight Flush pays 50-to-1
-
Four of a Kind pays 20-to-1
-
Full House pays 5-to-1
-
Flush pays 3-to-1
-
Straight pays 2-to-1
-
Three of a Kind pays 1-to-1
-
Two Pair is a Push
-
Others Lose
Here is the rack card (click on the image to make it larger):

As Michael Shackleford states on his page on DDP, the house edge for DDP is 6.7152%. Shackleford states that his results were obtained by a programmer, “JB.” I was fortunate to have previously written “two Joker” computer code back in 2006 that could be modified for this project. Nevertheless, programming this game was still a complicated task. It took me two days of conceptual thinking to figure out a programming strategy. After two more days of programming and debugging, it took my program took about 11 hours to complete the cycle running one thread, and just under 3 hours running four threads. After a few false starts, I came up with the same house edge as JB.
The following spread sheet lists the 172991 initial hands that can be dealt when playing DDP. Each hand lists the draw strategy for that hand, the number of “suit-permutations” considered for that hand, and the expected value for the hand.
The player who wants to know basic strategy for DDP can refer to this spread sheet and create his own version. I have not attempted to quantify basic strategy for DDP nor do I anticipate doing so. However, if you are interested in basic strategy, I refer you to this impressive strategy written by Michael Shackleford. Basic strategy for DDP is extraordinarily complicated and well beyond the ability of all but the most skilled players. In other words, if a player is using perfect DDP strategy, then he is doing something else to gain an edge over the casino.
With a baseline house edge of 6.72% and extremely complex basic strategy, the typical player is surely playing against an edge of 10% or more. I have not seen another casino table game that has as much going against it, from a pure edge/strategy viewpoint. The house edge for DDP could easily be lowered by improving the pay table for the Bonus bet. The game developer may have set the house edge at 6.72% knowing in advance that the game would be vulnerable to collusion.
The following table gives the combinatorial analysis for DDP, based on the poker-value of the initial five card poker hand that the player is dealt:
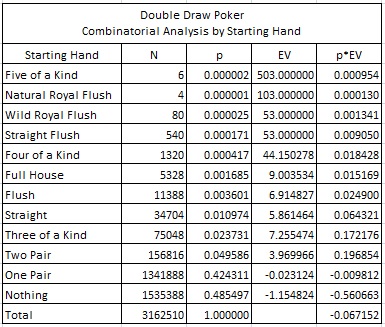
Note that 48.55% of the time, the player is dealt “Nothing.” For these hands, the house has an average edge over the player of 115.5%, based on the player’s Ante bet. In other words, if the player initially wagers $10 on the Ante and Bonus wagers (a total of $20) at the start of the hand, and he is subsequently dealt “Nothing,” then on average his expected loss is $11.55. The player would have to be dealt Two Pair off-the-top to have an edge over the house, on average.
A simple spread sheet computation using the spread sheet provided above shows that the house has the edge on 73.0501% of the initial five-card poker hands. The hand favors the player 26.9499% of the time. In other words, the player is dealt a long-term loser on about 73% of the hands he plays.
Another sobering view of the combinatorial analysis for DDP comes from breaking down the house edge by the number of Jokers the player is initially dealt:
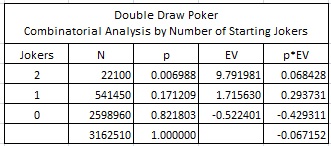
Looking at this table, we see that 82.18% of the time, the player will not be dealt a Joker. In this case, the casino’s edge will be, on average, 52.24%. If a player initially wagers $10 on the Ante and Bonus bets, and is subsequently dealt a hand without a Joker, he can expect to lose $5.22, on average. On the other hand, if the player is dealt one Joker, he can expect to win $17.16, on average. And, if the player receives two jokers in his initial hand (about 0.70% of the time this will happen), then he can expect to win $97.20, on average. In other words, it’s all about getting the Jokers. The game is a bust if the player is not dealt a Joker in his first five cards, and over 82% of the time he will not be dealt a Joker.
The table above also underscores one reason why collusion is so powerful in DDP. If six players receive no Jokers between them in their initial hands, then they are well-positioned to modify their drawing strategies.
Collusion analysis is usually completed by simulation, and that is how I proceeded for DDP. The simulations I conducted considered from one to six players seated at the table. It follows that the player seated at first base has knowledge of 5, 10, 15, 20, 25 or 30 cards before making his first draw decision. I also considered the player who is seated at third base. This player will get to see all the draws before him, and therefore may get to see up to an additional 15 cards before making his first draw decision. For this reason, I also simulated the collusion edge with knowledge of 35, 40, or 45 cards before the player makes his first draw decision.
The following table gives the results of my collusion simulations for DDP. I note that these results are for perfect collusion: the player has perfect information about all of the known cards and makes perfect strategic decisions based on this knowledge:
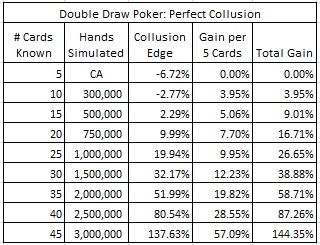
The third (middle) column gives the edge based on the given number of known cards. As few as three colluding players can get an edge over the house. With a full table of six players (30 known cards), this edge increases to more than 32% for the player at first base. As players around the table see more cards, the edge can get as high as 137.63% for the player at third base when making his initial draw decision.
The following graph gives a different perspective on these results:
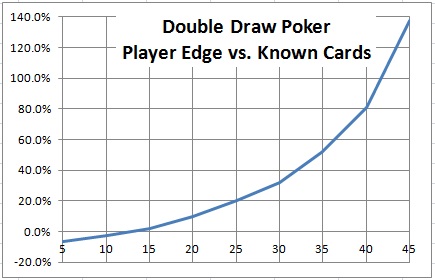
There should be no assumption or expectation that such edges can be achieved in practice. I personally have no idea how to go about creating a feasible collusion strategy for DDP. But, even if the players give back 75% of their edge based on sharing a reduced amount of information and using a simplified strategy, six colluding players are still going to eat up DDP.
My opinion is that DDP has an urgent game protection issue. Any casino that offers DDP should make sure that they have a “no sharing” policy in place and that this policy is strictly enforced. Staff and surveillance should monitor DDP for signs of player collusion. There is no easy fix for the game protection issues that DDP raises. Protecting DDP from player collusion will require vigilance.


