Flop Poker (FP) is a poker style game that is popular in the Southern states. First introduced in 2003, it is one of the longest surviving novelty games. FP is an example of a game that is both vulnerable to hole-carding and one that APs would not go out of their way to play. It isn’t enough to have an advantage. The advantage must be attainable without substantial bankroll and time requirements.
The rules for FP are as follows:
-
The game uses a single deck.
-
The player makes an Ante wager.
-
The player and dealer are dealt three cards, face down. The dealer’s cards are the “Flop.”
-
The player looks at his cards and decides to either play or fold.
-
If the player folds, he forfeits his Ante wager.
-
If the player plays, he must make a Flop bet equal to his Ante bet.
-
The dealer then turns up the Flop.
-
The best possible poker hand using all three of the player’s cards and any two of the Flop cards is made.
-
If the player has Jacks or Better, the Ante bet pays even money and the Flop bet pays according to a pay table.
-
If the player has less than Jacks or Better, then the player loses both the Ante and Flop bets.
Here is the most common pay table for paying winning Flop bets:
-
Royal Flush pays 1000-to-1.
-
Straight Flush pays 500-to-1.
-
Four of a Kind pays 100-to-1.
-
Full House pays 30-to-1.
-
Flush pays 20-to-1.
-
Straight pays 11-to-1.
-
Three of a Kind pays 4-to-1.
-
Two Pairs pays 2-to-1.
-
Pair of Jacks through Aces pays 1-to-1.
The following table gives the breakdown of the player final hands and house edge for a player using perfect basic strategy:
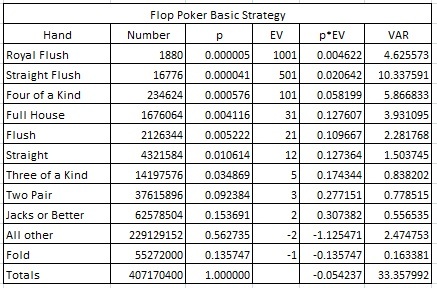
The baseline house edge for FP is 5.4237%. This is an extraordinarily high edge for a novelty game. In the column “p*EV,” the contribution of each final hand to the player’s return is given. Note that over 8.3% of the return of the game occurs on hands that are Four-of-a-Kind or better. These rare hands occur with frequency of about 1-in-1607 hands. What this means in practice is that if a player doesn’t hit any of these big hands, he will be experience an effective house edge of about 12.7%. In other words, the player is either losing big or winning big.
Just like Three Card Poker, the dealer deals packets of three cards to each player and to himself. It follows that this game has the same hole-card vulnerability as Three Card Poker. And indeed, when I observed this game, exposure of a hole-card was common. Using either the Ace shuffler or the iDEAL shuffler, opportunities will arise both because of table layout issues and sloppy dealer procedure.
In computing hole-card strategy, I wrote a computer program that cycled through all three card starting hands for the player together with every hole-card. Optimal strategy was then computed by cycling through each two-card group that could complete the remaining two cards of the flop. The data from this computation was sent to a file. I then culled the data to determine the strategy. Every time a new “Play” situation arose, I added a rule. Eventually it was clear that no new rules would arise.
Here is my strategy. Make a Play bet with any of the following, otherwise fold:
-
Any pair
-
Player's three cards are a flush
-
4 to a straight, e.g. (3/4/6/, 5)
-
4 to a gut-shot straight, e.g. (3/4/7, 5)
-
3 to a straight in player’s hand with 0 gaps and 1 high card, e.g. (2/3/4, J) or (9/T/J, 4)
-
3 to a straight in player’s hand with 1 gap and 1 high card, e.g, (2/3/5, J) or (8/T/J, 4)
-
1 high card in player’s hand and 1 high card in flop, e.g. (2/5/J, K)
-
2 or more high cards in player’s hand, e.g. (2/J/Q, 4)
The following table gives the breakdown of the player final hands and house edge for a player using perfect hole-card strategy:
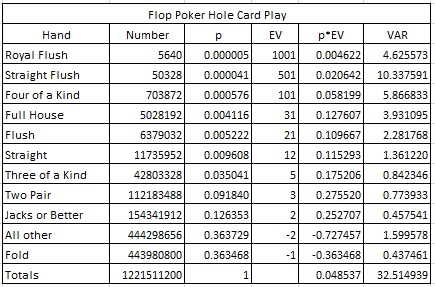
From this table we see that the player gets an edge of 4.8537% over the house if he uses perfect hole-card strategy. Just as important is the standard deviation, which is the square root of the variance. In this case it is 5.7022. A value this large indicates a huge swing in possible results for the AP. In particular, 8.3463% of the return for the AP is obtained by the hands that are Four-of-a-Kind or better. The premium hands occur with frequency of about 1-in-1607. The hand that contributes most to the variance is the Straight Flush that occurs 1-in-24271 hands. Just like the non-AP, the hole-card player will experience either a big loss or a big win.
Another observation from this table is that the player will fold 36.35% of his hands, and will lose two bets on 36.37% of his hands. It other words, the player will lose money on over 72.72% of the hands he plays. The most likely outcome is to lose two bets. He has a winning result on only about 27.28% of his hands.
This game is similar to Three Card Poker in the distribution of the results and high standard deviation. In Three Card Poker, the hole-card player will experience losing sessions until he hits his share of Straight Flush and Three-of-a-Kind hands. But FP is much more extreme. In Beyond Counting, James Grosjean states: “FP with knowledge of only one of the communal cards is a punishing game.”
Given the tremendous house edge attainable by hole-carding other games and the modest edge attainable by hole-carding FP, it is unlikely that an AP will target this game if only one hole-card is being exposed. Nevertheless, FP, like all games with a potential hole-card issue, should be protected. Here are my suggestions for protecting FP from hole-card play:
-
Learn hole-card strategy to be able to identify suspect play.
-
Frequently audit hole-card exposure on all proprietary games.
-
Frequently re-train and remind dealers of hole-card issues.
-
Re-configure tables that have poorly placed Ace/iDEAL shufflers.


