Heads-Up Hold'em (HUH) is a relatively new poker variant that seems to be gaining traction. Its rules are nearly identical to those of Ultimate Texas Hold'em (UTH) (see this post). I am surprised this game even exists. That said, HUH appears to be one of those rare games that has a real chance for success.
Recently a reader wrote to me via the contact form on this site and asked about hole-carding HUH. Because of the similarity between HUH and UTH, the programming I already did for hole-carding UTH is trivial to adapt to this new game.
Here are the rules for HUH. The key differences between these rules and those for UTH is that the "Blind" bet is now called the "Odds" bet, the player can only wager 3x pre-Flop, and there is a bad beat payout for losing with sufficiently good hands.
- The player makes equal bets on the Ante and Odds.
- Five community cards are dealt face down in the middle of the table.
- The dealer gives each player and herself a set of two starting cards, face down.
- Players now have a choice:
- Check (do nothing); or
- Make a Play bet of 3x their Ante.
- The dealer then reveals the first three community cards (the "Flop" cards).
- Players who have not yet made a Play bet have a choice:
- Check: or
- Make a Play bet of 2x their Ante.
- The dealer then reveals the final two community cards (the "Turn/River" cards).
- Player who have not yet made a Play bet have a choice:
- Fold and forfeit their Ante and Blind bets; or
- Make a Play bet of 1x their Ante.
- The dealer the reveals her two starting cards and announces her best five-card hand. The dealer needs a pair or better to "qualify."
There are many different situations that can arise after the hand completes. The dealer either does or doesn't qualify. The player's hand either beats, ties or loses to the dealer. All of this is similar to UTH. What distinguishes HUH is how the Odds bet (Blind bet in UTH) is handled. Unlike UTH, where the player loses the Blind bet if his hand loses to the dealer, in HUH, the player can win the Odds bet even if his hand loses to the dealer. This payout is called a "bad beat."
Imagine getting four of a kind and losing to a dealer straight flush in UTH. That situation must be extremely frustrating for the UTH player. In HUH, the player wins big when this happens (the Odds bet pays 50-to-1). In the most extreme case, suppose the player has the hand 9h/7d and the dealer has the hand Ah/4c. If the board is Th/Jh/Qh/Kh/3c, then the player's straight flush loses to the dealer's royal flush. In this case in UTH the Blind bet would lose, whereas in HUH the Odds bet pays 500-to-1. Note that both player cards don't have to play in the hand (unlike a bad beat jackpot in live poker).
- (Odds bet: player wins) If the player beats the dealer and the player's hand is strong enough, then he will win the Odds bet, otherwise the Odds bet pushes.
- (Odds bet: bad beat) If the player loses to the dealer and the player's hand is strong enough, then he will win the Odds bet (a "bad beat"), otherwise his Odds bet loses.
The following table is a summary of how HUH pays:
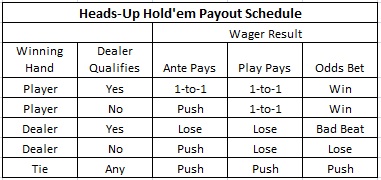
Here are the payouts for the Odds bet when the player wins the hand. Note that these are exactly the same payouts as for UTH:
- Royal Flush pays 500-to-1.
- Straight Flush pays 50-to-1.
- Four of a Kind pays 10-to-1.
- Full House pays 3-to-1.
- Flush pays 3-to-2.
- Straight pays 1-to-1.
- All others push.
Here are the payouts for the Odds bet when the player loses the hand (bad beat):
- Straight Flush pays 500-to-1.
- Four of a Kind pays 50-to-1.
- Full House pays 10-to-1.
- Flush pays 8-to-1.
- Straight pays 5-to-1.
- All others lose.
The following spreadsheet contains my full combinatorial analysis. It presents the 169 unique starting hands, together with the edge for checking and raising 3x. The sheet also gives the number of hands equivalent to the listed hand (the suit-permutations). For example, because the starting hand (2c,7d) is equivalent to (2h, 7s), only the hand (2c,7d) was analyzed.
In particular:
- The house edge for HUH is 2.35842%.
- The player checks pre-Flop on 68.62745% of the hands.
- The player raises 3x pre-Flop on 31.37255% of the hands.
- The player has a pre-Flop edge over the house on 38.15988% of the hands.
Pre-Flop Strategy
Here is a summary of pre-Flop basic strategy taken from the spreadsheet above:
- Raise 3x on the following hands, whether suited or not:
- A/2 to A/K
- K/7 to K/Q
- Q/T to Q/J
- Raise 3x on the following suited hands:
- K/4, K/5, K/6
- Q/8, Q/9
- J/T
- Raise on any pair of 3's or higher.
- Check all other hands.
Altogether in HUH, the player makes a 3x raise on 58 out of the 169 starting hands. In UTH the player makes a 4x raise on 69 of the 169 distinct starting hands. The following lists the 11 starting hands where the player checks in HUH but makes a 4x raise in UTH:
Offsuited: K/5, K/6, Q/8, Q/9, J/T
Suited: K/2, K/3, Q/6, Q/7, J/8, J/9
Flop Strategy
A Flop decision to check or raise 2x is only possible if the player checked pre-Flop. There are 111 starting hands where the player checked pre-Flop. I re-ran my HUH basic strategy program to consider each of these 111 hands and each possible Flop that can appear with that starting hand. For each starting hand when the player checked pre-Flop, there are combin(50,3) = 19,600 Flops to consider. Thus, altogether, I had to evaluate the Flop decision to check or raise 2x for 111 x 19,600 = 2,175,600 situations.
The following four spreadsheets contain the analysis for each of these 2,175,600 possibilities. Each spreadsheet contains the full data for roughly one-quarter of the starting hands.
To understand the data in these spreadsheets, the following image gives the first few Flop decisions for the player starting hand (9c, Qd) (see spreadsheet #3):
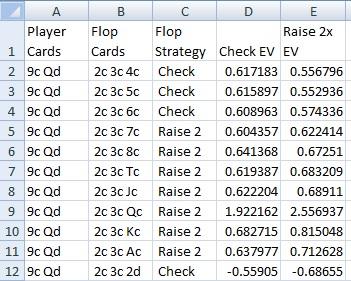
First consider 9c/Qd with a flop of 2c/3c/Qc. Obviously a 2x raise is correct here, with the pair of Queens. But there are some subtle hands as well. For example, holding 9c/Qd with a board of 2c/3c/6c, the correct play is to check, but if the board is 2c/3c/7c then it is correct to raise 2x. I have no intuition here.
As far as describing an overall strategy, Michael Shackleford recommends using his simplified UTH post-Flop strategy for HUH as well.
Shackleford's UTH strategy advises:
The player should raise 2x with two pair or better, a hidden pair (except pocket 2's) or four to a flush with a kicker of T or higher.
If the player is dealt any one of the 100 hands where the player checks pre-Flop in UTH, then the player will check that hand in HUH as well. Because of the identical nature of the betting structure on the Flop and Turn/River bets, these 100 hands should be played in HUH identically to how they are played in UTH. It follows that Shackleford's strategy directly applies in these cases.
Now consider the hand 9c/Qd. This hand should have a 4x raise in UTH but the player should check this hand in HUH. Consider what happens with Flop = (2c, 3c, 7c) when applying Shackleford's strategy. His strategy says to check this hand ("raise with four to a flush with a kicker of T or higher"), whereas row 5 of spreadsheet #3 (see the image above) shows that the correct play is to raise 2x.
Next consider the hand Jd/Tc. This hand also has a 4x raise in UTH but the player checks this hand in HUH. Now consider what happens with Flop = (2c, 3c, 8c). When applying Shackleford's UTH strategy, the player should raise 2x with this hand ("four to a flush with a kicker of T or higher"), whereas row 19607 of spreadsheet #3 indicates that the player should check this hand in HUH:
- Player hand = Jd/Tc
- Flop = 2c/3c/8c
- Check EV = 0.577282
- Raise 2x EV = 0.567261
- Basic strategy = check
There seems to be some work left to do to extend Shackleford's UTH strategy to the 11 equivalence classes of starting hands where the player raises 4x in UTH pre-Flop but checks in HUH pre-Flop. You have the spreadsheets, all you need is the patience and the strategy can be yours!
Turn/River strategy
If the player has checked both the pre-Flop and Flop bets, his last option is to either raise 1x on the Turn/River or else fold. As a reminder, here is Shackleford's UTH strategy, which he recommends for use in HUH as well:
The player should raise 1x when he has a hidden pair, or there are fewer than 21 dealer outs that can beat the player, otherwise he should fold.
I tried to think of an intuitively obvious exception to this rule arising from the bad beat payout on the Odds bet. I couldn't come up with one. If you can think of one, please post it in the comments. If you want to see my derivation of the "21 outs" part of this strategy, see this post.
Conclusion
The purpose of this post is not to lay out a perfect basic strategy for HUH. It is to set the groundwork for articles on hole-carding HUH. Like UTH, there are a host of different hole-carding situations to consider:
- One dealer hole-card.
- One Flop hole-card.
- One Turn/River hole-card.
- One dealer hole-card and one Flop hole-card.
- One dealer hole-card and one Turn/River hole- card.
- Two dealer hole-cards.
Collusion (information sharing) may also be possible.
What is true is that these hole-card computations are huge. Based on my UTH experience, each may take up to 8 days to complete. So I guess that still gives me plenty of time for trouble making.


