In this post, I asked for input on how Pai Gow Poker (PGP) could be legitimately beat by advantage players. An AP who posted under the name “jet” left a comment to that blog post, writing: “Actually people have beaten Pai Gow in the past. But don’t worry, that method isn’t applicable anymore, plus you aren’t going to figure it out any time soon…” He is right, I didn’t figure it out. But someone else did and he told me about it. As I will show, the AP’s method for beating PGP isn’t rocket science, but it is highly opportunistic and hugely profitable.
APs want a huge edge over the house, they want an edge with low volatility and they want a simple strategy. Using the method I will describe below, APs got all three and thoroughly crushed PGP. From what I understand, they continued to crush PGP for about five years until the method was discovered and corrective actions were taken. I was told that James Grosjean himself was involved in this scheme. For those of you who can’t wait to buy Beyond Counting, the method Grosjean used is not given in "the book" (at least, not that I could find).
Hole-card information about the dealer’s hand in PGP is essentially worthless. Dealers everywhere flash PGP hole-cards and no harm comes from it. Not only do dealers expose one (or more) of their own cards, but they also often expose one (or more) cards for each player hand. With cards being flashed everywhere, it is nevertheless the case that no meaningful edge can come from it. There are simply too many degrees of freedom in PGP to provide any real edge.
However, consider what it would mean if a player knew the bottom card of his own hand in advance of making a wager on his hand. In other words, imagine a situation where the player is dealt his cards before he makes a wager. Suppose that as the player's hand is dealt, the player’s hole-card is flashed so that the player knows a card that will be in his hand. After seeing this hole-card, the player can then choose how much to bet on his hand. You should see dollar signs spinning. But how could this possibly ever happen? How can the player hole-card his own hand in advance of making a wager?
Recall that PGP is dealt from a single deck of cards with a single semi-wild Joker. The Joker can take the place of an Ace, or it can be used to complete a straight or flush. If somehow the player does know a hole-card and the hole-card is an Ace or Joker, it’s clear the player’s hand will be very strong. At the very least, he would have a very strong top (two-card) hand. In this situation, the player would want to make a huge bet on his own hand. On the other hand, if the observed hole-card was a weak card then the player would make a table-minimum bet or possibly no bet at all.
This is precisely what happened on a special PGP betting opportunity called the “dragon hand.”
According to Wikipedia's article on Pai Gow Poker:
In some casinos … an extra "dragon hand" is dealt if a seat is vacant. After all players have set their original hand they are asked in turn if they would like to place another bet to play the dragon hand. Generally the bet on the dragon hand can be the table minimum up to the amount the player bet on their original hand ... generally the dealer turns over the dragon hand and sets it using the house way.
In particular, note the sentence, “the bet on the dragon hand can be the table minimum up to the amount the player bet on their original hand.” For the period 2007 to 2012, there was at least one casino that allowed players to wager any amount they wanted on the dragon hand up to the table maximum, irrespective of the player’s wager on his original hand. By making table minimum wagers on their own hands and table maximum wagers on the dragon hand when the dragon hand hole-card was a premium card, APs were able to effectively hole-card the dragon hand.
In other words:
- The AP sits at a table where there is no restriction on the bet size on the dragon hand.
- The AP makes a table minimum wager on his own hand.
- The AP sees a hole-card in the dragon hand.
- When there is a premium hole-card in the dragon hand, the AP makes a table maximum wager on the dragon hand, otherwise the AP makes no wager on the dragon hand.
The most important question is to determine how much hole-carding the dragon hand is worth. I have never written PGP analysis computer code, so answering this question would be a big project for me. I turned to two of the industry’s best, Charles Mousseau and Michael Shackleford, with a request for some simulations. I was amazed and delighted when they both jumped on the question and gave me their answers within a couple of hours.
I am indebted to gaming mathematician Charles Mousseau for providing the data in the tables presented below. I also thankful to Michael Shackleford for a simulation that confirmed some of Charles’ results.
As stated in the Wikipedia article, the dragon hand is usually set the house way. The following table gives the baseline house edge for PGP when the player’s hand is set using the house way. This table was created by simulating one billion (1,000,000,000) hands of PGP:
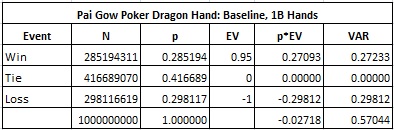
In particular, for the baseline situation, where no hole-card is viewed:
- The house edge in PGP if the player sets his hand using the house way is 2.718%.
- The standard deviation is 0.755.
We next move on to hole-card play. I am going to postpone giving the full combinatorial analysis and instead present the general discussion of advantage play for hole-carding the dragon hand. The player has an edge over the dragon hand whenever the hole-card is a Queen, King, Ace or Joker. The AP will play the table minimum on his own hand, and a table maximum bet on the dragon hand whenever the hole-card is a Joker, Ace, King or Queen.
The following table summarizes the player edge and standard deviation for each profitable hole-card:
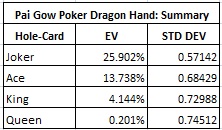
I am simply stunned by these results. The standard deviations are microscopic. Meanwhile, the AP’s edge over the house ranges up to an astronomical 25.902%. With a huge edge and very little bankroll risk, the money would be steadily moving towards the AP side of the table in this game. The only way it could get better is if the casino was giving away cash.
The following table shows the combined analysis for these four hole-cards:
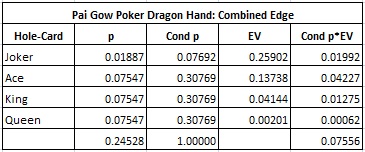
In particular, for the dragon hand with full hole-card exposure:
- The bet frequency is 13/53 = 24.528%.
- The average edge is 7.556%.
- The win per 100 hands is 1.853 units.
For example, suppose the table minimum is $10 and the table maximum is $1000. Then for 100 hands the AP will lose $10 x 100 x 0.02718 = $27.18 by playing the house way on his own hand. But the AP will earn $1000 x 1.853 = $1,853 by hole-carding the dragon hand. The AP’s net win per 100 hands is about $1,853 = $27 = $1,826. Now put a team of 5 APs on the table and they are taking over $9,000 per 100 hands off the table. This is demolition territory.
The fix that was put in place at the casino is the one embedded in the Wikipedia quote:
Generally the bet on the dragon hand can be the table minimum up to the amount the player bet on their original hand.
Let’s run the same analysis as above, but limit the dragon hand wager to the same wager as the main bet. Then, as noted above, the player will lose $10 x 100 x 0.02718 = $27.18 per 100 hands by playing the house way on his own hand. The AP will earn $10 x 1.853 = $18.53 per 100 hands on the dragon hand. The result is a net loss of $8.65 per 100 hands.
A skilled AP can get the house edge down significantly lower than the 2.718% figure that the house way yields. But even perfect basic strategy play by the AP will not yield enough to substantially beat the dragon hand. The game protection procedure of limiting the wager size on the dragon hand effectively shuts down this advantage play opportunity.
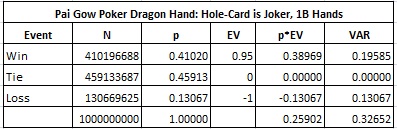
The following four tables show the combinatorial analysis for each hole-card, Queen, King, Ace or Joker. Each table is based on a simulation of one billion (1,000,000,000) hands of Pai Gow Poker.
Here is the analysis if the hole-card is a Joker:
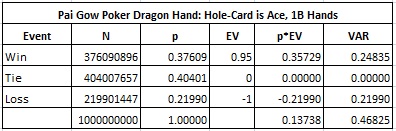
Here is the analysis if the hole-card is an Ace:
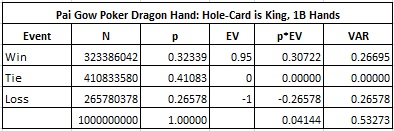
Here is the analysis if the hole-card is a King:
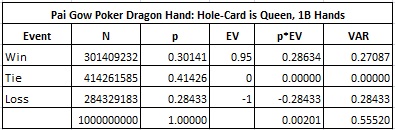
Here is the analysis if the hole-card is a Queen:
I was told that the AP team in question may have limited their play to the situations where either an Ace or Joker was in the hole-card. If that was the case, the following table shows the details of their edge:
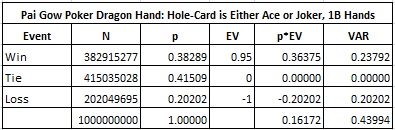
In particular, for the “bet the dragon hand on a Joker/Ace hole-card only” strategy,
- The bet frequency is 5/53 = 9.434%.
- The average edge is 16.172%.
- The win per 100 hands is 1.526 units.
I have long thought that APs found a way to beat Pai Gow Poker by some sort of hole-card play. It turns out that this is indeed the case, but it did not occur in a way that exposes an ongoing vulnerability. As I understand it, casinos continue to offer the dragon hand wager, but have imposed the restriction of limiting the dragon hand wager to not exceed the bet on the player’s main hand. This procedural change effectively shuts down the opportunity to beat the dragon hand.
The following is mandatory game protection for any casino that offers the dragon hand wager:
- The wager size for bets on the dragon hand must be limited by the amount the player wagered on their original hand.
This article would not have been possible without the help of three individuals.
I wish to thank the surveillance director who came forward with the information that APs had beat PGP by hole-carding the dragon hand. You provided incredible information to me without which this blog article could never have been conceived.


