Let it Ride Hole-Card Play

Let it Ride (LIR) is a game that has been in casinos since the time of the dinosaurs. Because the dealer is dealt two face-down cards, the question of hole-card play naturally arises. Back in 2002 at a Las Vegas strip casino, I found a dealer exposing a hole-card, but at the time had no idea how to play against it. I hardly knew the rules of the game and certainly had no clue about the strategy, so I passed the game by. In all the years since, I have never spotted another dealer exposing a hole-card on this game. The reason is simple: the dealing procedure has the dealer burning the bottom card of the three-card packet he deals himself. Because the bottom card is the one most likely to be exposed, multiple errors must be made for the AP to get a view.

But there is another lesson from that experience that is worth sharing. APs spend considerable time analyzing and learning new games. This is especially true of the most common games. The last thing an expert AP wants is to spot a hole-card on a game and not have the resources to take advantage of the opportunity.  Top APs are dedicated to their craft, and that means continually learning new material. If I was an expert AP at the time,  I would have known the information contained in this post and taken advantage of the opportunity.

The core idea of LIR is that the player is simply playing against a pay table based on the five cards he is dealt. He is required to make a wager without seeing any of his cards. That wager plays the whole way. Then the player has the option to make a bet against the pay table after seeing three of his cards. Finally, the player has the option to make a bet against the pay table after seeing four of his cards. These are three independent bets, each made against a fixed pay table. Because there is no “play or fold” requirement, there is no strategic dependence between these three opportunities.

The way this game is presented to the player, it looks as though the player is “taking away” the bets he doesn’t want to play, or leaving them out to “Let it Ride.” This is an illusion. Taking away bets is the same as placing bets. Either the wager is there or it’s not. For this reason, I will present the rules in a way that makes the independence of these wagers clear. This presentation may look odd, but understanding its equivalence to the usual way the rules are presented is the key to understanding the analysis of LIR.

Here are the rules to LIR:

1. The player makes a required ante wager.

2. The player is then dealt three cards face up and two cards face down.

3. The player can then make an optional flop wager based on seeing three cards.

4. The first face-down card is turned over.

5. The player can then make an optional turn wager based on seeing four cards.

6. The second face-down card is turned over.

7. Each of the player’s wagers (if made) is paid according to a fixed pay table.

Here is the most common pay table:

1. Royal Flush pays 1000-to-1.

2. Straight Flush pays 200-to-1.

3. Four of a Kind pays 50-to-1.

4. Full House pays 11-to-1.

5. Flush pays 8-to-1.

6. Straight pays 5-to-1.

7. Three of a Kind pays 3-to-1.

8. Two Pairs pays 2-to-1.

9. Pair of Tens through Aces pays 1-to-1.

10. All other hands lose.

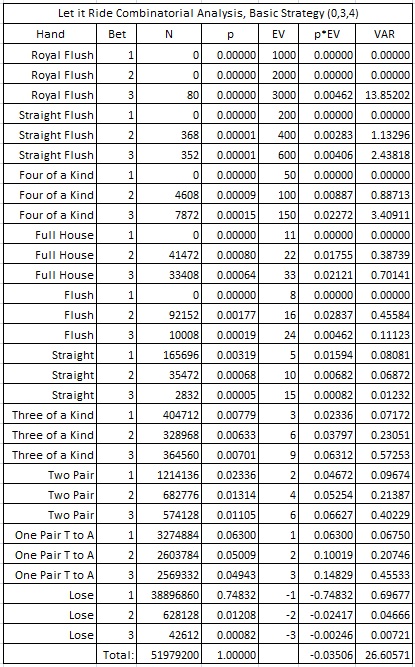
The analysis is quite easy from here. All we need to do is to get the edge when the player makes each wager and sum them. When the player acts, he will know either 0, 3 or 4 of the cards at the time of his wager. The AP may also know all 5 cards. Here are the edges:

• Player sees 0 cards: -37.272294%

• Player sees 3 cards: +10.912580%

• Player sees 4 cards: +22.854034%

• Player sees 5 cards: +38.849694%

For example, in the basic game, the player sees 0 cards before making his first bet, he sees 3 cards before making his second bet, and he sees 4 cards before making his third bet. Therefore the overall house edge is:

H/A = -37.272294% + 10.912580% + 22.854034% = -3.505680%

For each number of cards seen, there is an associated strategy for making the bet. This strategy applies to each bet separately and independently. This strategy applies whether the player sees a hole-card or is playing the game straight. Here is basic strategy:

Player bets knowing 0 cards: This is the initial bet. There is no strategy for this wager, it must always be made.

Player bets knowing 3 cards: This is the flop bet made after the player sees his three cards, without knowing either of the two down-cards. In a game where one of the down-cards is unintentionally exposed, the AP will always know at least 4 cards. Therefore, this strategy only applies to the base game, when no down-cards are known.

Here is the easy part of the flop bet strategy. Play the following:

• Any made hand (pair of Tens or better).

• Any straight flush, 345 through QKA. Do not play A23 or 234 suited.

• Any XYZ suited when each of X, Y and Z are Ten or better.

There are a number of additional hands that should be played. There are many ways to describe these hands using gaps and high cards. I’ll leave it to you to create whatever memory device works best for you.

Play the following suited hands:

• 78T, 79T, 7TJ

• 89J, 8TJ, 8TQ, 8JQ

• 9TQ, 9TK, 9JQ, 9JK, 9QK

Player bets knowing 4 cards: In a game where a hole-card isn’t exposed, this is the turn bet made after the player sees his three cards and one of the down-cards. In a hole-card game, the player will always know at least four cards after the ante bet, so this strategy is key to LIR hole-card strategy. It is also trivial.

Play the following hands:

• Any made hand (pair of Tens or better).

• Any four cards of the same suit

• Any open-ended straight 789T through TJQK (not JQKA)

Player bets knowing  5 cards: In this case it’s clear that correct strategy is to play with a pair of Tens or better.

It is now trivial to give the house edge for each combination of down-cards the AP might know in advance.

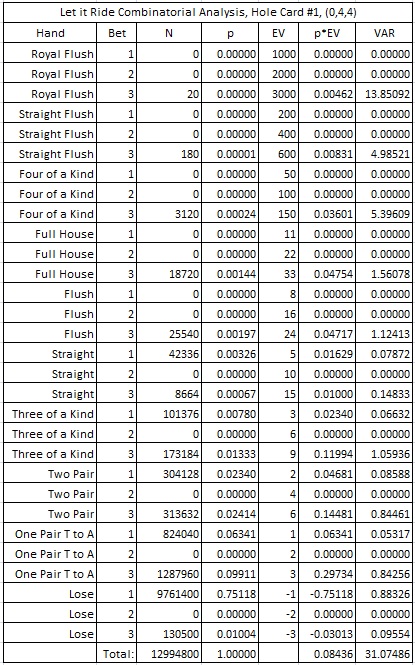
Hole-card situation #1: The AP knows the first down-card. In this case, the AP makes the required ante wager without knowing any of the five cards. His second wager will be made knowing his three cards and the first down-card (four cards). His third wager will also be made knowing his three cards and the first down-card (four cards), which was just turned up. The AP then knows 0 cards, 4 cards and 4 cards. It follows that:

H/A = -37.272294% + 22.854034% + 22.854034% = 8.435744%

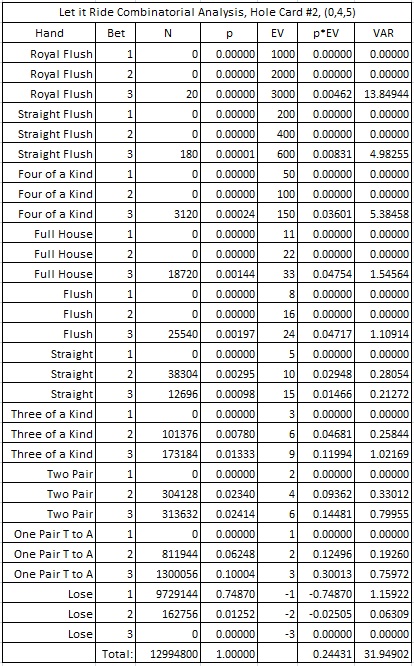
Hole-card situation #2: The AP knows the second down-card. In this case, the AP makes the required ante wager without knowing any of the five cards. His second wager will be made knowing his three cards and the second down-card (four cards). But after the first down-card is turned over, the AP will make his third wager knowing all five cards. The AP then knows 0 cards, 4 cards, 5 cards. It follows that:

H/A = -37.272294% + 22.854034% + 38.849694% = 24.431434%

Hole-card situation #3: The AP knows both the first and second down-card. In this case the AP makes the required ante wager without knowing any of the five cards. On his subsequent wagers he will know all five cards. The AP then knows 0 cards, 5 cards, 5 cards. It follows that:

H/A = -37.272294% + 38.849694% + 38.849694% = 40.427094%

Here is the complete combinatorial analysis for the basic game, the AP who knows the first down-card and the AP who knows the second down-card.  In particular, note the high variance. The player (or AP) experiences wild rides on this game. Regardless of being an AP or normal player there are long losing streaks while waiting for the big hands.

The following are my suggestions for protecting Let it Ride from hole-card play:

• Verify that correct dealing procedure is used.

• Audit dealers for hole-card exposure.

• Watch for players who are playing weak hands that are normally folded.

• Check all players who are wagering at or near the table maximum.