Mississippi Stud (MS) certainly has its share of game protection issues. For the savvy advantage player, just about everything works. There is one more method to beat MS that I have yet to discuss in this blog: player collusion. It's not a big play, but the fact that collusion is even possible comes as a surprise to many who operate the game. Indeed, some casinos deal MS face-up.
Normally, collusion requires that a significant number of cards be known to the players. For example, in Caribbean Stud, it requires 7 players to get a small edge (each player knows 30 cards in addition to his own five cards). In Three Card Poker, full information sharing with 7 players does not yield an edge (each player knows 18 cards in addition to his own cards). What is remarkable about MS is that collusion works at all. With 6 players, each player knows only 10 cards in addition to his own cards. But those 10 cards are plenty. By being able to wager up to 9 additional units, this limited amount of additional information can be leveraged to obtain a healthy edge over the house.
There is a long history of casinos dealing MS face-up. While this way of dealing MS protects it from card marking and edge sorting and increases game pace, a face-up game also makes collusion at a full table a triviality. Some APs just camp out at these games.
My effort here is to give results for collusion against MS using “perfect play.” With no additional information, the player knows 0 additional cards. This player is simply playing at the “house edge” of 4.91%. Playing a face-up game yields 10 additional cards. Maybe the AP also sees the burn card and therefore knows 11 cards. Maybe the table has spots for 7 players and he knows 13 cards. And so on …
To get the edges for all of these situations, I ran 16 simulations, consisting of the player knowing anywhere from 0 to 15 cards in addition to his own two initial cards. For each number of additional cards, I simulated a minimum of five million (5,000,000) rounds. Given the extremely high volatility for MS, even after 5M rounds the results I obtained are still only accurate to within about 0.2%.
Here are the results of my simulations:

For example, perfect collusion in a six-player face-up game gives the AP an edge of 2.29% over the house.
The following plot gives a graphical representation of the data in the previous table. In particular note that, on average, each additional card adds about 0.77% to the player's side:
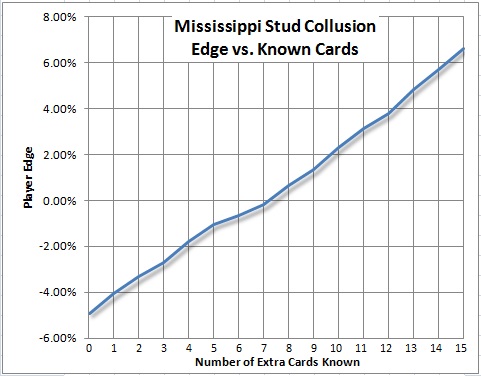
This graph may look linear, but clearly it is not. For example, if the edge gained by seeing additional cards was a linear function, then with 47 cards known the player's edge would be about -4.91% + 0.77%*47 = 31.3%. However, knowing 47 cards is the same as having perfect knowledge of the player's five cards, which gives the player an edge of 279.02% over the house (see this post).
This work is all very good in theory (and I am a theoretician at heart), but it leaves the question of a feasible strategy hanging unresolved. I don’t know the practical issues surrounding MS collusion. However, it is clear that perfect collusion strategy is not possible without computer assistance. The AP must give up a part of his edge to create a workable strategy.
Fortunately for the AP who wants to collude at MS, Stephen How created effective strategies for the six-player game. On his blog Discount Gambling, How has the following posts:
- Mississippi Stud @ Barona Casino, CA In this post, How gives a human-feasible six-player collusion strategy that gives the AP an edge of 1.5%
- Simplified Collusion for Mississippi Stud In this post, How gives an easy strategy for six-player collusion that gives the AP an edge of 0.5%.
I have no interest in recreating How's excellent work noted above. I contacted Stephen How and he graciously gave me permission to reprint his 1.5% strategy in this post.
How’s strategy uses the following definitions:
- “High outs” -- the number of cards remaining in the deck that will give you a high pair (Js thru As)
- “Mid outs” -- the number of cards remaining in the deck that will give you a mid pair (6s thru Ts)
- “Low outs” -- the number of cards remaining in the deck that will give you a low pair (2s thru 5s)
- “Suit outs” – for a suited hand, the number of cards remaining in the deck that are the same suit
- “Straight outs” – on the river bet, the number of cards remaining in the deck that complete a straight.
Here is Stephen How's six-player MS collusion strategy:
Flop bet:
- 3x raise a high or mid pair
- 3x raise with 6 high outs, or with 5 high outs and suited
- 3x raise a small pair with both trips outs still in the deck
- 1x call with 3 or more high outs
- 1x call with 2 high outs if suited, OR at least 2 mid outs, OR at all 3 low outs
- 1x call with 1 high out if suited AND at least 2 mid outs
- 1x call with at least 5 mid outs, OR suited and 4 mid outs
- 1x call with all 3 mid outs and all 3 low outs
- else fold
Turn bet:
- 3x raise any made hand
- 3x raise a low pair if no outs seen (no cards of your hand are out)
- 3x raise if suited and 8 or more high outs
- 3x raise if suited and 7 or more high outs AND 7 suit outs
- 3x raise if suited and 6 or more high outs AND 8 suit outs
- 1x call if suited
- 1x call if low pair and 2 trip outs
- 1x call if low pair and 1 trip out and at least 2 other pair outs
- 1x call if no-gap straight draw > 456
- 1x call if 1-gap straight draw and at least 5 mid outs
- 1x call if 2-gap straight draw and at least 6 mid outs
- 1x call if at least 4 high outs
- 1x call if 3 high outs AND (at least 2 mid outs, OR 1 mid out and all 3 low outs, OR all 6 low outs, OR wheel draw and 3 low outs)
- 1x call if 2 high outs AND (at least 4 mid outs, OR all 3 mid outs and 2 low outs)
- 1x call if 1 high out AND 5 mid outs
- 1x call if 7 mid outs, OR all 6 mid outs and all 3 low outs
- else fold
River bet:
- 3x raise any made hand
- 3x raise any flush draw
- 3x raise 8 straight outs
- 3x raise 7 straight outs AND (at least 3 high outs, or at least 4 mid outs)
- 3x raise 6 straight outs AND (at least 4 high outs, or at least 9 mid outs)
- 3x raise 5 straight outs AND (at least 6 high outs, or at least 12 mid outs)
- 3x raise 4 straight outs AND at least 8 high outs
- 3x raise 3 straight outs AND at least 10 high outs
- 1x call all other straight draws
- 1x call any low pair
- 1x call 5 or more high outs
- 1x call 4 high outs AND at least 2 mid outs
- 1x call 3 high outs AND at least 4 mid outs
- 1x call 2 high outs AND at least 6 mid outs
- 1x call 1 high outs AND at least 9 mid outs
- 1x call with all 12 mid outs, or at least 6 mid outs and a previous 3x raise
- else fold
Nobody said it was going to be easy. For the AP who wants to play against MS, it would surely be more worthwhile to seek out a dealer who is exposing a hole-card. But, if the situation is just right (e.g. the game is dealt face-up), there is no reason to expect that a savvy player wouldn't be just camping out.


