"Nothing could be smarter, more splendid, more brilliant, better drawn up than two armies. Trumpets, fifes, hautboys, drums, cannons, formed a harmony such as never been heard in hell."
-- Voltaire, Candide, Chapter 3
I do not know how Mississippi Stud (MS) has survived its crushing vulnerabilities to cheating and advantage play. Hole-carding gives the AP an edge from 55% to 104% over the house, depending on which of the three hole-cards is observed (see this post). Edge sorting gives the AP an edge from 40% to 66% over the house, depending on the group of cards being sorted (see this post). However, these two methods rely on knowing something about the dealer’s cards. This post addresses the edge an AP (or cheater) can get over the house if he has prior information about the cards he will receive.
With advance knowledge of the cards he will be dealt, the advantage the AP gets expires once he picks up his hand. At that point, he will complete the play of his hand using MS basic strategy. There is no special strategy the AP needs to learn when he has prior information about his own cards. The only decision that the AP can make that swings the edge his way is the size of his wager. In the best of all possible worlds, the AP would wager $0 when the known card(s) favors the house, and he would wager table maximum when the known card (s) favor the AP.
In MS, the player is dealt two cards. If he knows one of those two cards in advance, then the suit of the card he observes doesn’t matter. If he knows both cards, then there are two cases to consider. The first case is that the AP only knows the ranks (not the suits) of his two cards. The second case is that the AP knows both the ranks and suits of his two cards.
First, I consider the case when the AP knows one card in advance. In this situation, the AP just needs to know if the card he will be dealt favors the house or favors the AP. By observing the card on top of the first packet sitting in the automatic shuffler, and using a method such as edge sorting, the AP could get this knowledge. I refer to this method as “top carding.” I recently discussed using this method for Three Card Poker (see this post) and Caribbean Stud (see this post).
The following table gives the edges based on advance knowledge of one card in the AP’s hand:
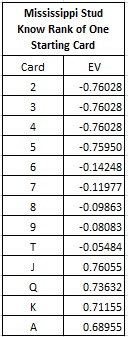
In particular, the AP has an edge when the top card is a J, Q, K, A, otherwise the house has the edge. The AP will make a large wager when the top card belongs to this group, otherwise he will make a small bet or no bet at all. The following table summarizes the edge and other statistics with optimal play given top card knowledge:
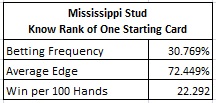
That 72.449% edge over the house looks pretty good. Unlike hole-carding or edge sorting, however, the AP doesn’t get that edge on every hand. He only gets that edge when he knows he will get dealt a premium card, which will be 4/13 = 30.769% of the time. It follows that an AP who uses an “all or none” approach to wagering will earn 100 x 72.449% x 30.769% = 22.292 units per 100 hands.
The posted win-rate of 22.292 units per 100 hands is an absolute maximum. In practice, the win-rate for the AP will be lower. I know for certain, based on a recent incident, that top carding has being used against MS.
The next situation I consider is when the AP knows the ranks of the two cards he will receive in advance. I confess that this information is purely academic. I have no idea how an AP (or even a cheat) might get this information and I have no reports from the field of this ever happening.
The following table gives the house edge based on prior knowledge of the ranks of the two cards the player is dealt:
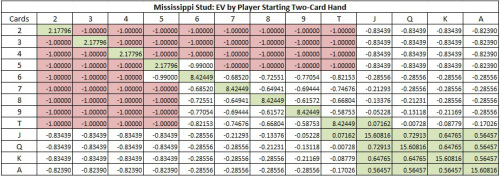
(click on the image to make it full size).
Here is the same table in pdf format: MS_Rank_Two_Known_Cards
The green cells indicate situations where the AP has the edge. The red cells indicate hands that basic strategy says to fold. The AP’s optimal strategy is to not play (or to make a table minimum bet) on any hand other than those in green. The AP should make a table maximum wager if he knows in advance that he will receive a green-shaded hand.
The following table summarizes the “green” hands:
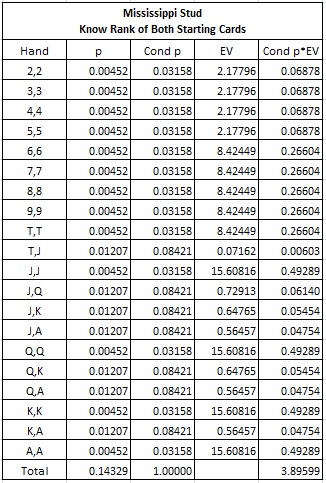
The following table summarizes the edge and other statistics if the AP uses optimal wagering strategy and knows the ranks of his two cards in advance:

An average edge of 389.599% is what gives APs (and cheats) the motivation to try to pull off this type of play. That fruit has to be incredibly tempting. The AP who makes a wager of $100 every time he has the edge, and otherwise sits out the hand, will earn $5583 in profit per 100 hands. As my dog would say, "woof!"
Perhaps the AP has the psychic power of precognition. Perhaps he has been taking some kind of drug that gives him x-ray vision. And maybe this is an abstract academic fantasy. And maybe you are a person who likes to read various random statistics about edges for proprietary games. Regardless, the following file gives the edges when the AP has advance knowledge of both the rank and suit of the cards he will receive:
By inspecting this file, the following table lists the two-card combinations when the AP has the edge:
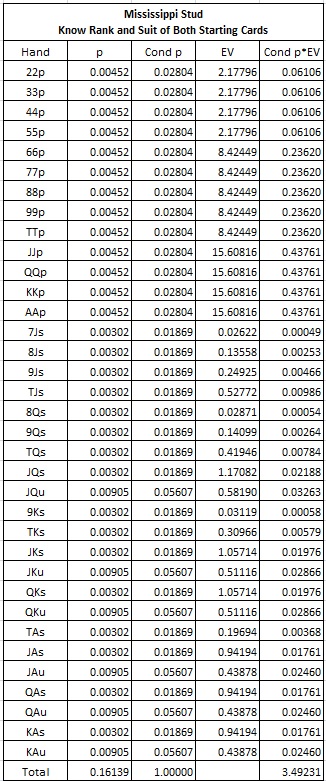
The following table summarizes the edge and other statistics if the AP uses optimal wagering strategy and knows the ranks and suits of his two cards in advance (the best of all possible worlds):
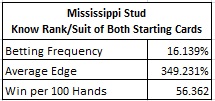
The surprising fact here is how little suit knowledge contributes to the AP’s win-rate. If the AP has advance knowledge of the ranks but not the suits of his two cards, the AP wins 55.825 units per 100 hands. Knowing both pieces of information gives the AP a win-rate of 56.362 units per 100 hands. Suit knowledge increases the AP’s win-rate by only 0.537 units per 100 hands. The reason for this small gain is that only a few rare marginal hands become playable. The lesson here is that the player who figures out a way of pulling off two-card advance knowledge should not concern himself with the suits of the cards.
In practical terms, this post addresses the situation of top card play, when the AP has information about one of his two cards in advance. The following procedures can be used to protect MS from top carding:
- Include a “turn” before the deck is placed into the shuffler.
- Do not feed the deck into the shuffler until all players have placed their wagers for the next round. Alternatively, a cut card can be placed on top of the first packet of cards after it is ejected from the shuffler so that the top of this card is not visible.
- Watch for a player at first base who has a large spread in his bets.
- Watch for team play to sort the cards and keep them sorted.
- Watch for signaling if the shuffler is located at third base.


