The table game Racing Card Derby (RCD) is meant to be dealt from a single deck of cards. I explored the “what if” of card counting RCD if dealt from an eight-deck shoe in this post. Card counting works on most games whose probabilities change as cards are dealt from a shoe. Whereas card counting is an after-effect of the rules and procedures of a game, hole-carding opportunities usually arise from sloppy dealing. This post explores advantage play against RCD when a card is known.
First, a review of the rules of RCD. To play a round, the cards are dealt, one at a time, and the suit of the exposed card is recorded. Cards continue to be dealt and exposed until one of the suits appears four times. The first suit to have four dealt is referred to as the winning suit, or simply, the “Winner.” The player can also wager on the color of the winning suit (red or black).
To complete the round, two additional suits must be dealt. First, additional cards are dealt until a suit other than the winning one appears. The suit of that card gives the 2nd-place suit. Additional cards are dealt until a suit other than the winning or 2nd-place suit appears. That is the 3rd -place suit. There are additional wagers based on these subsequent cards, called the “Exact Trifecta” and “Exact Quintella”.
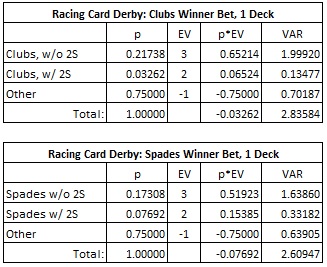
Clearly, true odds are 3-to-1. To generate a house edge the designers added a “protest card” rule. The payout to the player is reduced if the Two of Spades (2S) is dealt in the process of determining the winning suit. Here are the payouts:
- Player picks winning suit and no 2S is dealt: pays 3-to-1.
- Player picks winning suit and 2S is dealt: pays 2-to-1.
- Otherwise, the player loses.
Here is the combinatorial analysis of the Winner Bet for RCD when it is dealt from one deck:
In considering a known card, it is possible that the AP has knowledge of the top card (or any card that must appear in the hand). A top-card opportunity may arise because of sloppy dealing procedure, or it may occur from some other method, like edge sorting.
The following table gives the edge of each Winner Bet if the AP knows the top card:
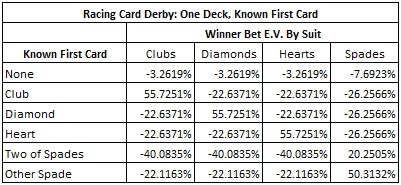
For example, if the top card is a Club, then a wager on the Winner Bet in Clubs gives the AP an edge of 55.7251%. If the top card is a Spade (not the 2 of Spades), then a wager on the Winner Bet in Spades gives the AP an edge of 50.312% over the house.
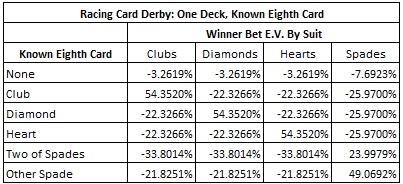
Knowing the top card yields tremendous advantages, but top card knowledge is a rare situation for the AP. Much more common would be to know the bottom card. If the AP has the opportunity to cut the cards after viewing the bottom card, he can cut that bottom card near the top. He will say something like "Thin to win!" The following table shows that even if the AP knows the card that is eighth from the top, he has a tremendous advantage by betting the suit of the card he observed:
If the AP observes the bottom card but is unable to cut after this observation, even this is enough for the AP to get a small edge over RCD. The following table gives the edge of each Winner Bet if the AP knows a card that will not appear in a hand (e.g. the bottom card, or by shuffle tracking).
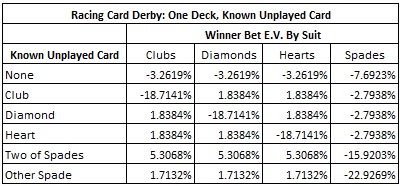
The best situation for the AP is if he knows that the 2 of Spades will not be played in a round. In that case, a wager on the Winner Bet in Clubs/Diamonds/Hearts yields a 5.3068% edge over the house. However, knowing any unplayed card in advance gives the AP an edge of at least 1.7132%.
There is no easy fix for card exposure issues. It is entirely up to the casino to insure that they are dealing RCD in a safe manner.


