One of the most massive games to analyze is Texas Hold’em Bonus Poker (THB). The game has a huge cycle, consisting of 55,627,620,048,000 (more than 55 trillion) different possible final hands. The cycle for hole-card play, knowing one of the dealer’s two cards, is even larger at 111,255,240,096,000 (more than 111 trillion) different possible final hands. Without making excuses, I’ve gone for too long without analyzing hole-carding for this game. This article begins to fill the analytical gap: hole-carding THB when one dealer hole-card is known.
In Beyond Counting Exhibit CAA, by James Grosjean, chapter 65 (pp. 367-371) is devoted to THB. More specifically, chapter 65 is devoted to certain shortcuts to basic strategy for THB. The material does not give a hint of hole-card strategy or the potential edge the AP can gain from hole-carding THB. Towards the end of the chapter, Grosjean teases the reader, saying,
“THB using basic strategy is not something we’re going to be playing very often, and not for big stakes. The most likely reason we might find ourselves in this situation at all is that we are waiting twenty minutes until our superior game resumes.”
What could Grosjean possibly mean by a "superior game?"
To begin with, I will review the rules for THB.
-
THB is played with a standard deck of 52 playing cards without jokers.
-
The player begins by making an Ante wager of one unit.
-
The player and dealer are each dealt two cards face down.
-
The player checks his cards, at which time he can either fold and forfeit his Ante wager, or make a Flop wager of two units.
-
Three community cards (the “Flop”) are dealt face up.
-
The player can either check or make an additional wager of one unit.
-
A single card (the “Turn”) is dealt face up.
-
The player can either check or make an additional wager of one unit.
-
A final card (the “River”) is dealt face up.
-
The player and dealer each make their best five-card poker hand from their two cards and the five community cards (Flop, Turn, River).
-
If the player’s hand beats the dealer’s hand and the player has a straight or higher, then the player is paid one-to-one on his Ante, Flop, Turn and River bets.
-
If the player’s hand beats the dealer’s hand and the player has less than a straight, then the player is paid one-to-one on his Flop, Turn and River bets. His Ante wager pushes.
-
If the player’s hand and dealer’s hand tie, then all bets are a push.
-
If the dealer’s hand beats the player’s hand, then the player loses all of his bets.
Basic Strategy
THB is very easy to understand and very tough to play correctly. I am not going to attempt to fully quantify basic strategy here. The resourceful reader can find this strategy online. However, the basic strategy decision for THB based on the player’s first two cards is trivial: the player should play every hand except the following off-suit hands: (2,3), (2,4), (2,5), (2,6) and (2,7).
The computation of basic strategy involves cycling through the 169 different possible starting hands the player can receive and computing the expected value for each. My program took about 82 hours to complete, running four concurrent threads. Here is a screen shot:
Just as the basic strategy program was completing its cycle, I figured out a way to make the program run almost twice as fast by creating a huge look-up table. I let the basic strategy cycle continue marching on to its natural conclusion, but I did use the improved computer code for the hole-card analysis.
The following pdf contains the expected value for each starting hand and house edge computation:
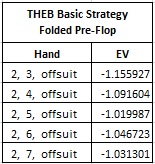
Note that with perfect strategy, the house edge is 2.036922%. The following table shows the hands whose expectation is less than -1.00, in other words, the hands that should be folded before the Flop:
Hole-Card Play
Next I will consider hole-card play. Assume the AP can see one of the dealer's hole-cards as the initial two cards are dealt to the dealer. The player’s hand has one of three possible types:
-
Non-suited non-pair. For example, (2c, 7d). The dealer’s hole-card can be the first suit, the second suit, or one of the other two suits. Generically, if the player’s suits are x and y, then the dealer’s suit is either x, y or z (z is one of the other two suits).
-
Suited non-pair. For example, (2c, 7c). The dealer’s hole-card can be the common suit or one of the other three suits. Generically, if the player’s suit is x, then the dealer’s suit is either x or y (y is some other suit).
-
Pair. For example, (Ac, Ad). Generically, if the dealer’s card is the same rank as the pair, then the suit of the dealer’s card is z (one of the other two suits). When the dealer’s card is not the same rank as the pair, then the suit of the dealer’s card can be x or y (the suits of the cards that make up the pair) or z (one of the other two suits).
Without any simplification, there are 66300 different combinations of player hands and dealer hole-card. By considering suit-permutations, this number can be reduced to 5083 different combinations. Computing the edge for hole-card play involves going through each of these 5083 starting hands and computing the expected value for each when played with perfect strategy. It took my program just over 43 hours to complete the computation.
The following pdf contains the full analysis of hole-card play for THB, when the player knows one dealer hole-card. Note that in those situations when the edge is less than -1.00, the player should fold without making a Flop bet.
This computation shows that the AP gets an edge of 7.607006% over the house for perfect hole-card play seeing one dealer hole-card.
The following pdf contains the 404 hands with expected value less than -1.00, in other words, the folded hands. These hands are listed by expected value for making the two unit Flop wager, from highest to lowest.
THEB_Hole_Card_1_Dealer_Card_Folds
Note that the hand combination that is weakest for the player is (2x, 7y) against the dealer’s Ty. For example, (2c, 7d) against the dealer’s Td. This hand has expected value -1.225732. The most borderline hand (edge closest to -1.00) is (4x, 8y) against the dealer’s Kx. For example, (4c, 8d) against the dealer’s Kc. This hand has expected value -1.000080.
This pdf file shows that the hole-card player should make a Flop wager with every suited hand, with the following exceptions:
-
(2x, 7x) vs. 8x, 9x, Tx, Jx, Qx, Ax
-
(2x, 8x) vs. 9x, Tx
-
(2x, 9x) vs. Tx
Note that (2x, 7x) vs. Kx has EV = -0.997, so the right strategy is to Play.
The following table gives the full hole-card strategy for the Flop wager for unsuited hands. Those squares colored red represent hands that should be folded: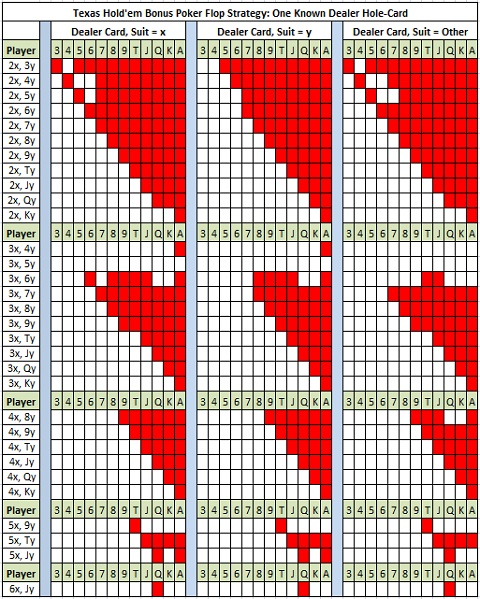
If the AP plays basic strategy for his pre-Flop wagers, and perfect post-Flop hole-card strategy, the AP will have an edge of 6.714744% over the house. In other words, the pre-Flop strategy above is worth only 0.892262%. This strategy, by itself, is not enough to give the AP the edge. By contrast, post-Flop strategy is worth 8.751666% to the AP. The post-Flop wagers are where the AP leverages the majority of the information gained by knowing one of the dealer's hole-card.
There is no question that THB suffers a significant risk to hole-carding. Reading between the lines in Grosjean’s remarks, it appears that this vulnerability is well-known to some APs and that APs have actively targeted THB in the past.
I recommend the following:
-
Check the positioning of the shuffler on the layout. The shuffler should be unobstructed and be placed on the opposite side of the table from the discard tray.
-
Routine audits of dealers for hole-card issues.
-
Watch for big players who make highly unusual plays, in other words, the “lucky idiot.”
-
Watch for signaling and team play on games with big action.


