I know it must seem like I am drunk, given the way I keep analyzing over-the-top AP opportunities. How could it be possible to see both of the dealer's hole-cards in Texas Hold'em Bonus Poker (THB) at the start of the hand? I was recently contacted by a surveillance professional at a casino where this exact scenario took place! He told me that THB was hand dealt at his casino. Nothing wrong with that, just don't deal any cards until they are absolutely needed! He was writing a report on an incident and wanted to know the edge the APs got. By a weird coincidence, I recently considered this same hole-card scenario for Ultimate Texas Hold'em (UTH) (see this post). In this modern era, even the most unexpected things happen.
I previously wrote about the situation where the AP can see one dealer hole-card in THB in this post. I wrote about the situation where the AP can see one dealer hole-card and one common card in THB in this post. I ran a complete combinatorial cycle for the first case (one dealer hole-card), but I did the second analysis by running simulations. This post considers the situation when the AP sees two dealer hole-cards. I completed this analysis by running a full cycle.
To begin with, I will review the rules for THB:
- THB is played with a standard deck of 52 playing cards without jokers.
- The player begins by making an Ante wager of one unit.
- The player and dealer are each dealt two cards face down.
- The player checks his cards, at which time he can either fold and forfeit his Ante wager, or make a Flop wager of two units.
- Three community cards (the “Flop”) are dealt face up.
- The player can either check or make an additional wager of one unit.
- A single card (the “Turn”) is dealt face up.
- The player can either check or make an additional wager of one unit.
- A final card (the “River”) is dealt face up.
- The player and dealer each make their best five-card poker hand from their two cards and the five community cards (Flop, Turn, River).
- If the player’s hand beats the dealer’s hand and the player has a straight or higher, then the player is paid one-to-one on his Ante, Flop, Turn and River bets.
- If the player’s hand beats the dealer’s hand and the player has less than a straight, then the player is paid one-to-one on his Flop, Turn and River bets. His Ante wager pushes.
- If the player’s hand and dealer’s hand tie, then all bets are a push.
- If the dealer’s hand beats the player’s hand, then the player loses all of his bets.
Without further delay, here are the results when the AP can see both dealer hole-cards prior to making his pre-Flop (play/fold) decision:
- The AP gets an edge of 29.8539% over the house.
- The AP plays 87.7379% of the hands.
- The AP folds pre-Flop 12.2621% of the hands.
Pre-Flop strategy
When the AP can see both dealer hole-cards pre-Flop in UTH, it was easy to write down a pre-Flop strategy (see this post). Unfortunately in the corresponding situation, no simple play/fold pre-Flop strategy exists for THB.
The starting hand with the negative EV if played is:
- Player = (2c, Kd), Dealer = (Kc, Kh), Play EV = -2.688040
The starting hand that is closest to being played, but should be folded, is:
- Player = (2c, 9d), Dealer = (Td, 7d), Play EV = -1.000006
To get a full sense for the pre-Flop strategy mess, just look at these images taken from the combinatorial analysis spread sheet given above: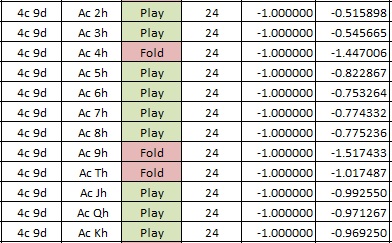
For example, the AP should fold (4c, 9d) against (Ac, Th) but play against (Ac, Jh). The dealer having two over-cards against the AP is not sufficient to indicate a fold.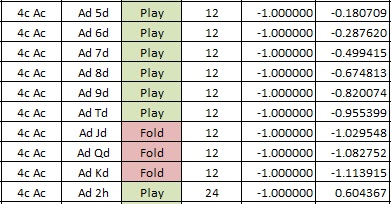
For example, the AP should play (4c, Ac) against (Ad, Td), but fold against (Ad, Jd). The dealer dominating the AP is not sufficient to indicate a fold.
Flop/Turn strategy
For all the complexity that goes into deciding whether to play or fold pre-Flop, the Flop and Turn bets are straight forward. These are independent wagers that each pay even money whenever the player wins the hand. There is no obligation to make these wagers to complete the hand. Therefore, the AP should only make these wagers when he has a greater chance to win the hand than the dealer, otherwise he should check.
After seeing the three Flop cards, there are 45 known cards from which two will be taken to complete the board (Turn and River cards). If the AP could quickly run a mental cycle, going through the combin(45,2) = 990 two-card combinations, then his decision would be easy. If more of these combinations favor the AP than the dealer, then the AP should make the Flop wager. Otherwise he should check.
Another method is to use the "rule of 4". Figure out the total outs left for the player to beat the dealer and multiply that number of outs by 4 to get the percent chance of winning the hand. Count "runner-runner" combinations as 1 out.
Finally, the Turn wager couldn't be easier. The AP will know his hand, the dealer's hand, the three-card Flop and the Turn card. There are 44 cards left in the deck from which one will be dealt as the River card. If more of these cards favor the AP's hand than the dealer's hand, then the AP should make the Turn wager.
Conclusion
Game protection advice? I've got none. But, there are many morals to this story. Pick the one you think best applies ...
- Mistakes are a part of being human. Appreciate your mistakes for what they are: precious life lessons that can only be learned the hard way. -- Al Franken
- Remember that failure is an event, not a person. -- Zig Ziglar
- What to do with a mistake - recognize it, admit it, learn from it, forget it. -- Dean Smith


