Ultimate Texas Hold'em (UTH) is one of the most popular novelty games in the U.S. For example, only Three Card Poker and Let it Ride have more placements in Nevada. What makes UTH so successful is its similarity to Hold'em poker together with the chance for a huge payday if the player makes a top hand. There are a number of advantage play opportunities against UTH, foremost of which is hole-card play. With the dealer receiving two hidden cards, and with five hidden Flop and Turn/River cards, the astute AP may acquire significant information in advance of making his betting decisions. Edges over 20% are possible. In my opinion, UTH is second only to Mississippi Stud (see this post and this post) in its overall vulnerability.
As a reminder, here are the rules for UTH (taken from this document):
- The player makes equal bets on the Ante and Blind.
- Five community cards are dealt face down in the middle of the table.
- The dealer gives each player and herself a set of two starting cards, face down.
- Players now have a choice:
- Check (do nothing); or
- Make a Play bet of 3x or 4x their Ante.
- The dealer then reveals the first three community cards (the "Flop" cards).
- Players who have not yet made a Play bet have a choice:
- Check; or
- Make a Play bet of 2x their Ante.
- The dealer then reveals the final two community cards (the "Turn/River" cards).
- Player who have not yet made a Play bet have a choice:
- Fold and forfeit their Ante and Blind bets; or
- Make a Play bet of 1x their Ante.
- The dealer the reveals her two starting cards and announces her best five-card hand. The dealer needs a pair or better to "qualify."
Now what? Well, either the dealer qualifies or she doesn't. The player beats, ties or loses to the dealer. Either the player's hand is good enough to qualify for a "Blind" bonus payout, or it isn't. The following table hopefully clarifies all of these possibilities and gives the payouts in every case:
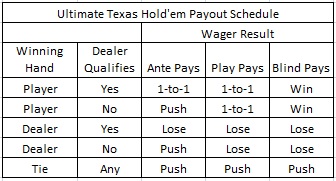
The final piece of the puzzle is the Blind bet. As the payout schedule above shows, if the player wins the hand, regardless if the dealer qualifies, then the player's Blind bet is paid according to the following pay table:
- Royal Flush pays 500-to-1.
- Straight Flush pays 50-to-1.
- Four of a Kind pays 10-to-1.
- Full House pays 3-to-1.
- Flush pays 3-to-2.
- Straight pays 1-to-1.
- All others push.
In preparing for my hole-card computer analysis, I wrote a program to analyze the basic game as described above. I computed that a full cycle would require analyzing 10,634,692,068,000 (10.6 Trillion) unique hands. This computation would require about 4 days to complete on my four core i-7 Ubuntu computer.
Here is a summary of the statistical results for UTH, assuming perfect strategy:
- The house edge is 2.18497%
- The standard deviation is 4.93931
- The hit frequency (winning 1 or more units) is 46.5699%
- The modal (most common) result is to Fold and lose 2 units. This happens on 19.1816% of the hands.
Here is Michael's simplified basic strategy (s = suited)
Pre-Flop Strategy (Check or Raise 4x):
- Check every non-paired hand with a high card of 3, 4, 5, 6, 7, 8, 9, T.
- Check all J2 through J7. Raise J8s and J9s. Raise all JT.
- Check Q2 through Q5. Raise Q6s and Q7s. Raise all Q8, Q9, QT and QJ.
- Raise K2s, K3s, K4s. Raise all K5, K6, K7, K8, K9, KT, KJ, KQ.
- Raise every hand containing an Ace.
- Check 22. Raise every pair 33 through AA.
Flop Strategy (Check or Raise 2x):
- Raise with two pairs or better.
- Raise every pair 33 through AA.
- Raise with four to a flush when the player's cards include a T or better of the flush suit.
- Otherwise, check.
Turn/River Strategy (Raise 1x or Fold):
- Raise with any pair.
- Raise when there are 20 or fewer dealer hole cards that will cause you to lose the hand based on your hand and the community cards.
Following the strategy outlined above, Michael states that the house edge is 2.43%.
In Exhibit CAA, James Grosjean has some very interesting things to say about computing basic strategy and hole-card strategies for UTH. Grosjean wrote (pages 358 and 359),
There are three approaches to devising a strategy for a game such as UTH. The first approach, preferred by the AT (advantage theoretician) is to let a computer cycle through every combination of cards, making the perfect decision as each possible card is dealt. The "optimal edge" calculated using this combinatorial analysis will be reported with many digits and great fanfare, sometimes accompanied by a boast about how many days it took the computer to accomplish the Herculean feat of calculating the gazillion possibilities ...
Unfortunately for those of us who actually wish to win a few bucks playing these games, we do not have the computational abilities of the computer, nor will we be using a computer in a casino. For a real player, the "optimal edge" provided by the AT is worthless. The only value of this "optimal edge" is that it gives us an upper bound on what a human-feasible strategy could deliver, indicates whether further research is likely to be fruitful, and provides a debugging tool for other researchers to verify that their own computer programs do indeed replicate the result.
The second approach, really an extension of the first, is to derive a human-feasible strategy by grouping the gazillion possibilities into a manageable number of categories, along with rules on what the player should do in each situation ...
Facing the uselessness of the computer's "optimal strategy," and the complications of the case-oriented strategy, we turn to a third hybrid approach. We will provide certain descriptive categories with rules that can be pre-memorized, but for other areas that get messier, particularly when the player has nothing but kickers on the river, we will incorporate the method of counting outs ... The method of counting outs is quite accurate if applied to the river decision.
It is clear that Shackleford's basic strategy follows Grosjean's third "hybrid" approach, by giving exact Pre-Flop and Flop strategies, while counting "outs" for the Turn/River decision.
What is curious about Grosjean's comments, however, is that they are in the chapter on UTH. Throughout Exhibit CAA and Beyond Counting, Grosjean publishes pages of computer-perfect strategies for dozens of games. One has to look no further than his presentation of the strategy for play against Texas Hold'em Bonus Poker to see the lengths he will go to write out computer-perfect strategy. Indeed, on page 371 of Exhibit CAA, Grosjean wrote,
Admittedly, the strategy charts are messy. THB has the most complicated basic strategy of any casino game. Many players will not have the willingness, need, or ability to learn the complete set of rules, though a printed BS card count possibly include them all. The more rules we apply, the closer we get to computer-optimal strategy.
For UTH, Grosjean did not compute the "gazillion possibilities." It appears that based on some limited computational results, Grosjean created human-feasible hole-card strategies for UTH. With his strategies in hand, Grosjean then let a computer program determine the approximate edges by means of simulations. In particular, Grosjean gives the following information in Exhibit CAA:
- Knowing both of the dealer's hole cards, the AP gets an edge of "about" 35.00%.
- In the case when the AP knows one dealer hole-card, Grosjean gives a hybrid strategy, but declines to give the edge the AP gains from using that strategy. I was told it is in the 12% to 13% range.
- Knowing one of the dealer's hole cards and one Flop card, Grosjean reported that his strategy yields an approximate player edge of 20.74%, but no exact information is given.
- Knowing one of the dealer's hole cards and one Flop/River card, Grosjean stated that his strategy gives an approximate edge of 24.10%, but no exact information is given.
James, it's okay that you didn't run complete cycles. You are both an extraordinarily gifted "AT" and "AP." Just because the "AT" part of you didn't feel like doing the work, doesn't mean that the "AP" had to make excuses. UTH is big.
Personally, I love the smell of a hot computer in the morning, as it burns through tera-cycles computing optimal strategies. As an "AT," all I care about are exact results and I am happy to let my computer run for days to get these results. I have often posted log files from my computations and advised the curious reader to devise his own strategies based on that information. Knowing the exact answer to a question is never the wrong approach.
As of this writing, I have a computer program running the case where the player knows one dealer hole-card prior to his pre-Flop decision to check, raise 3x or raise 4x. The program has been running for about 68 hours on four cores, and it has about another day to go until it completes. Here is a screen shot, using the "top" command, somewhere in the middle of computing the gazillion possibilities:
UTH has been on my "to do" list for almost three years. I'm finally doing it! Over the next few weeks, I hope to write a series of posts where I explore various combinations of initial information that might be available to the AP. Each computation will take about 5 to 7 days to complete (current estimate). My goal in each case will be to determine precise player advantages and to give computer-perfect pre-Flop (check, raise 3x, raise 4x) strategy in each case. I will present the strategies in the form of downloadable spread sheets that the AP can cull if he wants to create his own simplified strategy.
No excuses.


