Ultimate Texas Hold'em (UTH) has a significant hole-card problem (see this post and this post). I've wondered for a long time if it also has a collusion problem: if players are allowed to share their cards at the table, can they get an edge? For the would-be colluder, players don't have many cards to share. A full table with six spots only gives players a total of 12 cards to work with. On the flip side, the strategy for UTH is based around "outs;" cards that make the player's or dealer's hand. It doesn't take that much information to switch the value of a hand through a wide range of EVs.
For many years I thought that the "Tablemaster" version of UTH was beatable outright by APs using collusion:
To collude, five APs play at the machine. Because their cards are dealt face-up, they can each view all of the 10 face-up cards. The players could take their time, discussing their possible strategy changes, without the pressure of the pit boss or dealer to make a decision. If collusion worked, this would be the ideal situation to take a shot.
About 3 years ago, I read a brief message board discussion about these machines. One AP asked if there were any of these games left in Las Vegas. Another AP answered that the last one he knew about had recently been taken out. The first AP then stated, "I guess the last gravy train has left the station." Through these comments, these APs made it clear that the Tablemaster version of UTH held some sort of worthwhile opportunity, though they didn't say what it was. I had always assumed these APs were talking about collusion. Now I am not so sure.
In a live casino version, UTH is dealt on both 5 and 6 spot tables (from images.google.com):
To explore the possibility of collusion at UTH, I only considered the six-spot case. There were two reasons for this choice. First, if UTH is not vulnerable on a six-spot table, then clearly the five-spot table is safe as well. Second, the computer simulation for six-spot UTH collusion is substantially faster than the five-spot case. In other words, I could generate more data faster.
I note that analyzing collusion must be completed by simulation; a full six-spot collusion cycle would require consideration of 53,328,385,406,769,300,000,000 possibilities, consisting of two player cards, 10 common cards, 3 Flop cards, 2 Turn/River cards and 2 dealer cards. If I could have access to every computer on the planet to run this cycle, I could get it done in a few days. I finally have a good reason to try to take over the world ...
... Having not taken over the world, I proceeded by simulation. This is the point in the post where I concede that my work here is not sufficient. In my opinion, an accurate assessment of collusion would require simulating about 100,000 hands. I only simulated 500 hands. Let me explain why I stopped at 500.
To simulate just one possible starting configuration (2 player cards, 10 other known cards) requires the evaluation of 3,915,147,600 (3.9 billion) possibilities. To simulate a single starting configuration required about 25 minutes of computer time on my dedicated Linux box. I ran four instances of the program concurrently, allowing me to simulate four hands every 25 minutes. Do the math and it took just over 52 hours (2 days, 4 hours) to simulate 500 hands. My computer needs to do other things, and two days of simulation was enough. For reference, for my program to simulate the required 100,000 hands would have required 434 days. Or, if I owned 434 computers, it would have taken 1 day.
Okay, you've read enough preamble. Here are the (very approximate) results for six-player collusion at UTH:
- The six-player collusion edge at UTH is about 2.5%.
- Collusion strategy violated basic strategy on the pre-Flop decision on 47 out of the 500 hands.
- When collusion strategy violated pre-Flop basic strategy, the average EV gain was about 11.2%.
Here is an example where the player checked pre-Flop when basic strategy says to raise 4x.
Example 1.
- Player = Js, Ts
- Common cards = 4h, Jc, Jd, 2h, Td, Th, 9c, 8c, 7h, 6s
- Check EV = 33.54%.
- Raise 4x EV = -12.17%.
To gain some intuition for the reason that basic strategy was violated, note that four outs to make a player-pair are in the common cards. Moreover, there are no over-card outs in the common cards (these are outs that the dealer can use to make an over-pair). This makes the likelihood of a dealer over-pair much higher. The effect of this information on the edge is dramatic. Violating basic strategy improves the player's EV in this situation by 45.71%.
Here is an example where the player raised 4x pre-Flop when basic strategy says to check.
Example 2.
- Player = Kc, 3h
- Common cards = 5h, 4h, 2s, 9h, Ts, 8d, As, 9d, Jc, 6s
- Check EV = 7.96%
- Raise 4x EV = 28.86%.
In this case, there are no "pair outs" in the common cards, meaning that making a pair is much more likely for the player as the hand plays out. Moreover, the common card "As" is an over-card that can beat the player if the dealer holds an Ace. That common card means one fewer over-pair out for the dealer. Violating basic strategy improves the player's EV in this situation by 20.89%.
The following images give the details for each of these 47 hands (click on the image to make it larger):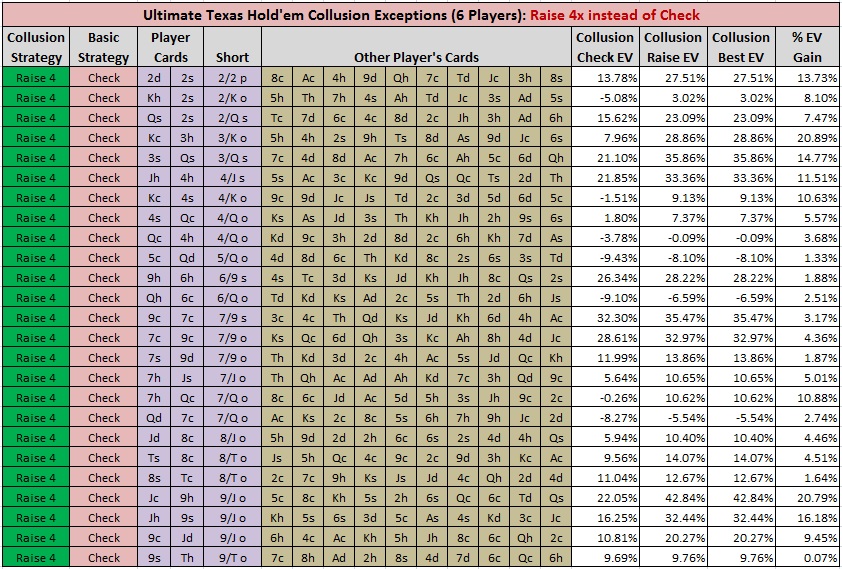
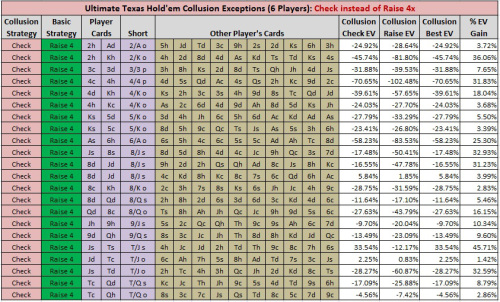
You can find full details for my 500-hand simulation in the following spread sheet:
Given the complexity of a human-feasible UTH collusion strategy, an approximate six-player edge of 2.5% is simply not sufficient to generate interest by advantage players. Moreover, given this result, the five-player game is unlikely to yield any collusion edge at all. When collusion against games like Double Draw Poker (see this post) can yield an edge of 30% or more, that 2.5% looks very small.
Although I don't think a collusion team will ever attack UTH, knowing outs will still have a tangible effect on the house edge for the astute player. For this reason, it is completely reasonable to have a "no sharing" rule at UTH tables. In other words, there should be a policy that players shouldn't share their cards with each other or otherwise discuss their hands. However, even if players do share their cards, management shouldn't be concerned.
Simply put -- don't sweat collusion at UTH.


