Ultimate Texas Hold'em (UTH) is a rich source of advantage play opportunities. This post considers yet another possibility: when the player knows one of the two cards he will be dealt in advance of placing his initial bet. I often refer to this knowledge as "top carding," though the known card can be either player card. Knowledge of one player card can be gained, for example, by edge sorting, accidental exposure, card location, skilled cutting, shuffler issues, incidental marks on the cards and outright cheating. Whatever the means, the edge the player can get is extraordinary.
The work presented here is based on the combinatorial analysis I completed for the main game (see this post). No specialized computer analysis was required. After all, once the initial wager has been made, the hand will be played according to basic strategy. The only advantage the AP gets is whether his known card favors the player or the house.
The following table shows the edge, based on the known card:
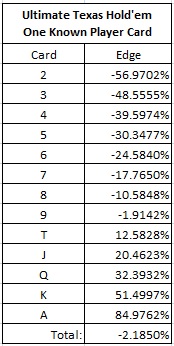
Note that the average edge across all known cards is -2.1850%, the house edge (last row in table). If the known card is a Ten, Jack, Queen, King or Ace, then the AP has the edge, otherwise the house has the edge. The AP exploits this knowledge by making a large wager when he has the edge, otherwise he will either make a small wager or sit out the hand.
After I completed this work, I decided to check my results against those presented by James Grosjean in Exhibit CAA (page 362). I was surprised to discover that our results don't agree. For example, I give an edge of -56.97% if the known card is a Deuce. Grosjean gives an edge of -57.96% in this same situation.
Here are Grosjean's known card results:
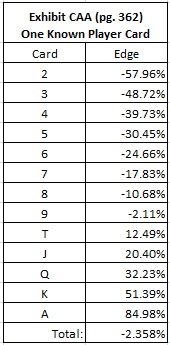
Note that Grosjean'saverage edge across all known cards is -2.358%, which is NOT the house edge (last row in table). It follows that Grosjean's results are not correct. I do not mean this to be a gotcha against Grosjean -- I am simply making a methodological point. These differences reinforce theconjecture I've made in other posts that Grosjean's UTH results were obtained by simulation and not by exhaustive analysis. These differences are not consequential to the AP. (Note. As David Spence commented below, it appears that Grosjean's numbers may bebased on his basicstrategy with house edge 2.35%, and not computer-perfect basic strategy.)
The following table gives the statistics for known card play against UTH:
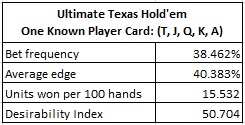
Knowledge of one card is a stronger opportunity than hole-carding. Even if the AP knows one dealer hole-card and the Turn/River hole-card, he "only" has an edge of about 25%. An average edge over 40% is a good day. A desirability indexof 50 puts this play in the stratosphere (Note: I used the overall standard deviation for UTH when I computed the DI, not the standard deviation when the hand is restricted to containing one of the cards, T, J, Q, K, A.).
The following procedures can be used to protect UTH against known-card advantage play:
- Include a turn before the deck is placed into the shuffler.
- Do not feed the deck from the previous round into the shuffler until all players have placed their wagers for the next round.
- Watch for a player at first base who has a large spread in his bets.
- Watch for team play to sort the cards and keep them sorted.
- Watch for signaling if the shuffler is located at third base.
- Watch for dirty and marked cards.
- Replace the cards if something just doesn't look right and hole-carding has been excluded.


