That's right, I kid you not! For about a month, a Las Vegas casino offered a baccarat side bet with a misprinted pay table that gave the player a 10.32% edge over the casino. Just sit at the table, make the side bet and collect your profit. You could be sipping mojitos on the beach at Shake Joe's in Samara, Costa Rica right now.
A few weeks back, I learned about a new side bet at an off-strip casino in Las Vegas, the gananam side bet (GSB) [Note. gananam is a Hindi word meaning "that which cannot be named."]. GSB was being discussed on a popular Internet gambling message board. GSB pays based on the sum of the point values of the Player hand and Banker hand, which is a total between 0 and 18. If the final sum is 0, 1, 2, 3, 15, 16, 17 or 18 then the player wins, otherwise the player loses. Like the Total Shot Bonus (see this post), it occurred to me that GSB should have some card counting vulnerability.
I had some extra time on Monday (July 6), the day before my Advanced Advantage Play seminar. I decided to pay the casino a visit and have a look for myself. Here are three images from the casino that show the pay table that was printed on the felt:



[Note. I did not take these pictures. They came from a poster who put them up on the message board where this bet was being discussed.] Don't be confused by the layout. This is really just one wager. The pay table is spread out on a banner that is similar to the "insurance" banner in blackjack. The player makes his GSB wager by placing his bet on the banner in front of his own wagering area. As is evident from the pictures of the layout, here is the pay table:
- Total = 0 pays 51-to-1
- Total = 18 pays 26-to-1
- Total = 1, 2, 3, 15, 16, 17 pays 2-to-1
- All other totals lose.
I had a hard time believing that this pay table was really being used, so I introduced myself to a pit boss and asked about it. I was told that staff found it very difficult to accurately pay this side bet. Whenever there was a 51-to-1 or 26-to-1 payout, the dealer was instructed to divide the wager up into red chips and green chips then pay off each stack separately. Still, something just didn't look right. No game inventor would make weird payouts like that. When I returned to my room a few hours later, I computed the combinatorial analysis for the GSB. Imagine my surprise when I finished:
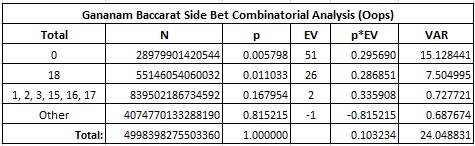
In case you can't read what's going on here, let me summarize in bold red font:
- The player has a 10.3234% edge over the house on every hand!
Here is a picture of the mojito you could be drinking:

Here are a few more facts about GSB with the pay table above:
- The standard deviation is 4.9040
- The hit frequency is 18.4785%
- The desirability index is 21.05
Obviously there was a misprint on the layout. But what happened to cause this misprint? There are two ways that wagers pay out in casinos. One is "x-to-1" and the other is "x-for-1." In table games, most wagers pay "x-to-1." What this means is that if the player wins, his original wager is returned and he is paid x additional units. For example, in blackjack, insurance pays 2-to-1. If the player wins his insurance bet, then his original wager is returned and he is paid 2 additional units. In the table game universe, it is rare to find a wager that pays using a "x-for-1" mechanism. One example occurs in baccarat; the Tie bet is typically printed on the layout as 9-for-1. The following was taken from Google images:

When the player makes a Tie bet, if the hand ends in a tie, then the player's original wager is collected, and he is subsequently paid 9 units. They key is that the player forfeits his original wager. This is exactly how slots and video poker work as well. A moment's thought will convince you that "9-for-1" is exactly the same as "8-to-1." So the Tie bet simply pays 8-to-1. Do you see what happened with GSB now? Evidently, the game creator, or the mathematician, or someone in marketing, or someone in casino management thought it would be a good idea to have GSB pay in a "x-for-1" format, similar to the Tie bet. All the pays on this layout were meant to be "-for-1", not "-to-1." That is, the intention was that GSB would pay 51-for-1, 26-for-1 and 2-for-1. To see the effect of this printing error on the payouts, note that:
- 51-for-1 is the same as 50-to-1
- 26-for-1 is the same as 25-to-1
- 2-for-1 is the same as 1-to-1
Having the bet pay 50-to-1, 25-to-1 and 1-to-1 would be a natural choice for the game developer. It would also be easy for the dealer to pay winning bets with these odds. That was the intention all along. Printing the layout with either 51-for-1 or 50-to-1 would have been sufficient to make the math work and the dealer happy. Printing the layout with 51-to-1 invited disaster. Here is the combinatorial analysis for the intended pay table:
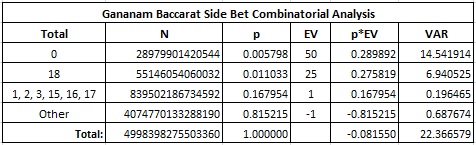
In particular:
- The house edge is 8.1550%.
- The standard deviation is 4.7293.
- The hit frequency is 18.4785%.
That's a nice house edge, right where it should be, just over 8%. Mistakes happen. Some are more expensive than others. This one was an opportunity of historic proportions. When I visited, it was my impression that APs had not yet found this side bet. You missed your chance. I told them about the goof. No mojitos for you!


