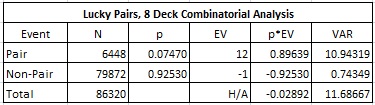
In this post I described beating the Lucky Pairs (LP) baccarat side bet. The method I described was called “Targets and Weights.” In that post, I considered the case when a pair pays 11-to-1, with a baseline house edge about 10.36%. For many ordinary players, that edge is too high for them to be interested in playing LP. As a result, the wager is underutilized. One option to get more action is to increase the payout to 12-to-1. This will have the dual effects of making the wager considerably more interesting to the average player, while also making the game considerably more vulnerable to advantage play.
Here is the combinatorial analysis when a pair pays 12-to-1, assuming an eight-deck baccarat shoe:
The first consideration when offering LP is the possibility of perfect play. In a brick-and-mortar game, perfect play can only occur through nefarious methodologies. But, if an AP finds a 12-to-1 opportunity on live-play online baccarat, then it is easy for the AP to gain this edge. The following table gives the results of a simulation of one hundred million (100,000,000) baccarat shoes, assuming perfect play.
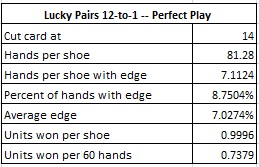
As a reminder, here are the details from perfect play in the 11-to-1 version: the AP who makes a LP wager of $100 on both the Player pair and Banker pair whenever he has the edge, and at no other time, expects to earn about $37.54 per shoe. If the AP if he finds a 12-to-1 game, he is now earning $99.96 per shoe. This represents a 274.7% increase in income for the online-AP.
In the brick-and-mortar world, a human-feasible methodology is necessary. I previously presented the “Targets and Weights” method. That method applies equally well here. In this method, the AP keeps track of the number of remaining cards (frequency) of each rank on his scorecard. When there are 60 or fewer cards remaining in the shoe, the AP then assigns a “weight” to each frequency. The AP then sums the weights, and if that sum exceeds the target value for the number of cards remaining, then he makes the bet. That is, the AP makes the LP wager whenever:
(Sum of the Weights) ≥ Target (Eq. 1)
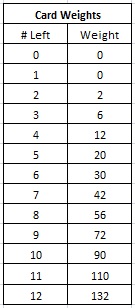
The following table gives the weights for each rank-frequency. If there are 13 or more cards left of any rank (with 60 or fewer cards remaining), then the AP always makes the LP wager. These values are identical to those for the 11-to-1 version of LP.
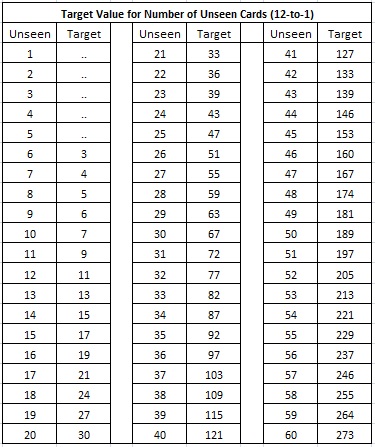
The following table gives the target values based on the number of cards remaining in the shoe. If there are 61 or more cards left in the shoe, then the AP never makes the LP wager. These targets are generally lower than those given for the 11-to-1 version of LP.
The following table gives the results of a simulation of one hundred million (100,000,000) baccarat shoes using the Target and Weights method. In this simulation, I assumed that the player made a one unit wager on each of the Player pair bet and Banker pair bet whenever Eq. 1 was satisfied (2 units total); otherwise no LP wager was made.
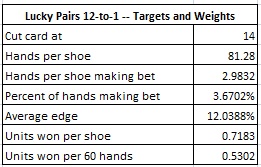
We see from these results that using Targets and Weights, the AP will make the LP wager on about 3.67% of the hands he plays, and when he makes the LP wager, his average edge will be about 12.04% over the house. Assume that the AP makes a LP wager of $100 on both the Player pair and Banker pair ($200 total) whenever he has the edge, and at no other time. Then this AP can expect to earn about $71.83 per shoe in the long run ($53.02 per hour). This is compared to the optimal value of $99.96 per shoe. The Target and Weights method yields over 71% of the return from perfect play, which represents significant inefficiency. The reason for this inefficiency is the increase in opportunities to make the LP wager beyond 60 cards with the 12-to-1 payout that don’t occur as often with the 11-to-1 payout.
The following are my suggestions for safeguarding LP from advantage play:
- Increase the cut-card depth to at least 26 cards.
- Do not expose the initial burn cards.
- Watch for players who make the LP wager late in the shoe, who bet on both sides, and who make table maximum wagers.
- Watch for players who keep score in a manner that indicates rank tracking.
- Watch for players who scratch mathematical sums on their score cards.
- Watch out for exploiting weak hand-shuffles through shuffle tracking.


