The Royal Match (RM) wager is one of the oldest blackjack side bets still available. It pays if the player’s first two cards are the same suit. If the cards form the rare hand KQ suited, then there is a premium payout. It is intuitively clear that there must be situations where the player has the edge. Quantifying the value that can be obtained through practical methods is where the work of the AP begins.
Research on beating this bet dates back to the early 1990s. For example, an article written by John Leib titled “Royal Match and the Davies Counting System” was published in “Blackjack Forum” (Vol. XIV #1, March 1994). At the time, playing against RM was a viable alternative source of income for the AP. Unfortunately for the AP, Leib assumed a single-deck game with 7 rounds dealt between shuffles. In the modern era, that game is nearly impossible to find.
Like the 21 + 3 wager, it is reasonable to disregard the premium hands in looking for an edge and focus on maximizing the most common outcomes. There are two counts that approach RM in this way, the "Red/Black Count" and the "Difference Count."
In the first edition of Beyond Counting, James Grosjean analyzed the Red/Black Count. This method assigns the value +1 to Diamonds and Hearts (red cards) and -1 to Clubs and Spades (black cards). If the count is sufficiently positive, then a black suited pair is more likely. If the count is sufficiently negative, then a red suited pair is more likely. The Red/Black count is similar to the "Rank Count" I suggested for the Pair Square blackjack side bet in this post. Grosjean’s results show that the Red/Black count typically returns about 25% to 30% of the theoretical maximum return available from computer-perfect play.
In the second edition of Beyond Counting, Grosjean considering a new count called the “Difference Count.” He stated: “The Difference Count trounces previous counts for Royal Match … In a deep, heads’ up game, the system performs quite well …” Grosjean’s results show that The Difference Count typically returns between 70% and 80% of the theoretical maximum available from computer-perfect play.
This post gives details for the Difference Count.
The Difference Count requires that the AP keep track of the number of cards remaining in each suit. The “running count” is RC = (Max – Min), where Max and Min refer to the number of cards remaining in the most and least abundant suits, respectively. As usual, the “true count” (TC) is obtained by dividing RC by the number of decks remaining. The trigger count is the minimum value of the count such that the AP should make the RM wager. In multi-deck games, the true count is used. In single-deck games, the running count is used. The Difference Count is similar to the count I described to target flushes in the "21 + 3" blackjack side bet. Details were given in this post.
For example, in a single-deck game, if the number of each suit remaining is Clubs = 9, Diamonds = 6, Hearts = 4, Spades = 7, then Max = 9, Min = 4, so the running count is RC = 9 – 4 = 5. There are 26 cards (1/2 deck) remaining, so the true count is TC = 10.
There are different pay tables for the single-deck and two/six-deck versions. The single-deck pay table is 10/3 (KQ suited = 10, suited = 3). The multi-deck pay table is 25/2.5. Here is the combinatorial analysis for each: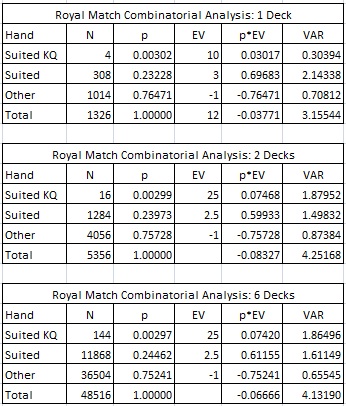
From the combinatorial analysis given above, the two-deck and six-deck versions have significantly higher house edges than the single-deck version. Moreover, the AP may struggle keeping track of multiple suits through multiple decks. For this reason, it is highly unlikely the AP will focus on the multiple-deck versions. Unfortunately, there aren’t many single-deck games that are worth playing. Finding a single-deck game that pays 3:2 for blackjack, has the RM bet, and gives a reasonable number of rounds per shuffle is like looking for a small diamond in a pail of sand. If the AP finds that game, it is even more unlikely that the casino will also allow a bet on the RM over $25.
To begin our discussion of beating the single-deck version of RM using the Difference Count, first recall that single-deck blackjack is almost never dealt with a cut card. Instead, a certain fixed number of rounds are dealt based on the number of players at the table. Heads-up, the most common number of rounds between shuffles is five, though this number can vary considerably by dealer, casino, and geographic region.
The following table assumes a heads-up single-deck game and gives the results based on the number of rounds per shuffle. Each column was computed based on a simulation of one hundred million (100,000,000) single-deck shuffles.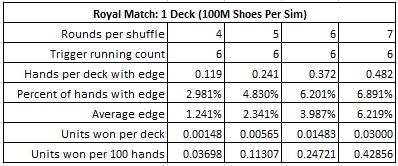
For example, in a heads-up single-deck game, playing at a game with four rounds dealt between shuffles, the AP should make the RM bet whenever the RC is 6 or higher. In this case he will wager on about 2.98% of the hands he plays, and will have an average edge over the house of 1.24% when he makes the bet. If the AP finds a fast heads-up game, getting 200 rounds per hour, and makes a $100 wager every time he has the edge, the AP will earn about $7.37 per hour. With five rounds per deck between shuffles, the AP will make $22.61 per hour. Six rounds pays $49.44 per hour and seven rounds yields $85.71 per hour.
In this era, the most common heads-up game an AP will find will allow a $25 maximum bet on RM and five rounds (or fewer) per shuffle. In this case, the AP will earn about $6.55 per hour, making RM hardly worth the effort.
It is worth comparing the return of the single-deck version with the multiple-deck versions. The following tables give details of simulations of the RM for two decks and six decks: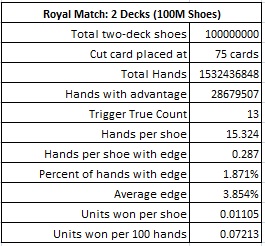
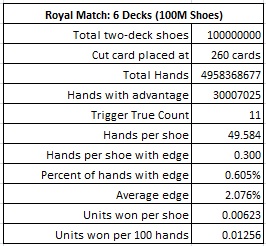
For example, in the two-deck game, the AP should make the RM bet whenever the TC is 13 or higher. In this case he will make the wager on about 1.87% of the hands he plays, and will have an average edge over the house of 3.85% when he makes the bet. If the AP finds a fast heads-up game, getting 200 rounds per hour, and makes a $100 wager every time he has the edge, the AP will earn about $14.43 per hour playing against the RM wager. On the six-deck version, the AP will earn about $2.51 per hour playing against the RM wager. Compare these values with $22.61 available for the single-deck version, 5 rounds per shuffle, and it is clear why the AP seeks out the single-deck game. On the other hand, with a clump of suited cards and a weak shuffle, there may be a much stronger method against a multi-deck game available.
There was a recent exception to the viability of the six-deck game. Stephen How discovered a casino that offered the six-deck version of RM with a top payout of 75-to-1 for suited KQ and 2-to-1 for other suited hands. This version has a much smaller house edge of 4.056%, but very large variance. Because of the premium payout for KQ suited, this bet is highly vulnerable to a count that tracks Kings and Queens. This is similar to the vulnerability of the now-defunct “Super 7’s” bet or the crushable Slingo side bet. Stephen discovered that a simple true count of Kings and Queens would yield a strong edge for the player. His article is given here: Counting The Royal Match Sidebet @ Barona Casino.
The following are my suggestions for protecting the Royal Match blackjack side bet:
- Deal at most 5 rounds per shuffle in a heads-up single-deck game.
- Evaluate players who only play RM late in the shuffle at a table maximum bet.


