Last week I attended and presented at the Cutting Edge Table Games Conference at Paris Casino in Las Vegas. The turnout this year was strong and the number of vendors who showed off their games spiked up significantly. Along with SHFL and Galaxy Gaming, there were more than 20 other independent table game inventors showing their games. As part of the conference, there was a contest for “Best New Table Game.” In the past, this award has been won by outstanding games such as High Card Flush, War Blackjack, EZ Baccarat and others. Each of these winners has demonstrated market success.
The winner of the “Best New Table Game” award this year was a conglomeration of blackjack side bets called “Pick ‘Em Blackjack.” In addition to his blackjack wager, the player can make one or more of the following three wagers:
- The “17 Bet.” This wager wins if the dealer busts, is a push if the dealer gets a total of 17, otherwise the player loses. A winning wager is paid 3-to-2.
- The “18 Bet.” This wager wins if the dealer busts or has a final total of 17, is a push if the dealer gets a total of 18, otherwise the player loses. A winning wager is paid 1-to-1.
- The “19 Bet.” This wager wins if the dealer busts or has a final total of 17 or 18, is a push if the dealer gets a total of 19, otherwise the player loses. A winning wager is paid 1-to-2.
The “18 Bet” used to be called “Instant 18.” I have not previously analyzed card counting Instant 18, the reason being that I thought this side bet was extinct. For reference, card counting Instant 18 was analyzed at discountgambling.net. The present post concerns card counting the 19 Bet.
Aside from the fact that Pick ‘Em Blackjack won first place, what drew my attention to the 19 Bet was the documentation given out at the developer's booth. In their documentation, the developers included specific information about the vulnerability of the 19 Bet to card counting. I am grateful that many game developers now take game protection seriously and go the extra mile. Whether a game ends up having issues or not, developers owe this due-diligence to their prospective clients.
The following is the complete text of the card counting analysis included in the documentation for Pick ‘Em Blackjack provided at the conference:
Counting systems were tested by an independent mathematician. We can discuss further if you are interested in the specifics. The 18 Bet was the most thoroughly tested and also has proof of working in a casino. All of these are countable, but to a much less degree than a standard hand of blackjack. Using a nearly perfect counting system, 9.283% of hands are playable for the 19 Bet, which is still far lower than the over 25% of playable hands for a standard game of blackjack. The 9.283% of hands is utilizing a counting strategy of
- 2, 3, 7, 8, 9 = -1
- 4, 5, 6 = 0
- 10, A = +1
I refer to the card counting system given in this documentation as System #1. In other words,
System #1 = (1, -1, -1, 0, 0, 0, -1, -1, -1, 1).
Focusing on the 19 Bet, the main claims in the documentation are as follows:
Claim #1: System #1 is “nearly optimal.”
Claim #2: The bet frequency is 9.283%.
I contacted the developer of this game for more specifics about this analysis. Listed below are some of my questions and the answers provided by the additional information I received.
Question 1: How many decks were used in this simulation?
The results are based on card counting a six-deck shoe. Note that the 19 Bet will be more vulnerable if dealt from a two-deck shoe and it will be less vulnerable if dealt from an eight-deck shoe.
Question 2: Was the simulated game H17 or S17?
The results given are based on the H17 rule. Note that the 19 Bet will be more vulnerable if the dealer stands on Soft 17 (S17), because the average dealer final hand will be slightly lower.
Question 3: What was the depth of the cut card in the simulation?
I couldn’t find the answer to this question in the documentation I received. In an email communication, I was told that the cut card was placed 40 cards from the end (at a depth of 272 cards) in a six-deck shoe.
Question 4: How many six-deck shoes were simulated?
The documentation I received stated that one billion (1,000,000,000) hands were simulated. In a six-deck shoe game, approximately 50 hands per shoe will be played with the cut card at 40 cards. This yields about 20M simulated shoes. I typically simulate somewhere between 100M and 1B shoes so that any statistical noise smooths out.
Question 5: What is the win-rate for card counting the 19 Bet?
Although the bet frequency is provided in the documentation, no other information about the win-rate is given. Knowing how often hands have positive EV is a necessary piece of the puzzle, however it is not sufficient. For example, Lucky Ladies (2 Decks) has a bet frequency of 7.2% and the player wins 1.17 units per 100 hands. Conversely, Dealer Bust 21 has a bet frequency of about 19.5% but the player wins only 0.59 units per 100 hands. A higher bet frequency does not necessarily mean a higher win-rate.
There is no indication that this question was addressed in the analysis. Unfortunately, without quantifying the win-rate, the analysis is essentially meaningless.
Question 6: Are the results accurate?
By the “results” I refer to claims #1 and #2 above. I will address the accuracy of these claims after I present some preliminary information and my card counting analysis.
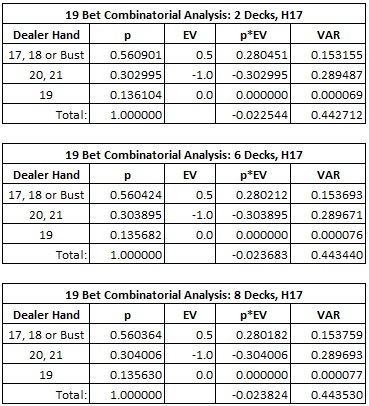
To begin with, the following tables give the combinatorial analysis for the two-deck, six-deck and eight-deck versions of the 19 Bet, assuming the dealer hits soft 17:
The following table gives the EOR’s and a card counting system for the six-deck version:
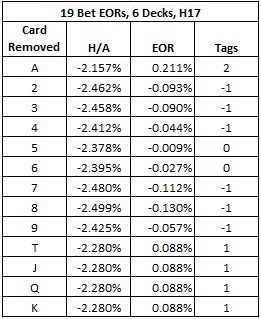
A reasonable card counting system based on these EORs is:
- 2, 3, 4, 7, 8, 9 = -1
- 5, 6 = 0
- T, J, Q, K = +1
- A = +2
In other words, an alternative card counting system to System #1 given by the developers is:
System #2 = (2, -1, -1, -1, 0, 0, -1, -1, -1, 1).
This is very close to the System #1 given above. The only tags that differ are those for Aces and Fours. The accuracy of a card counting system can be measured by computing what is known as the “Betting Correlation.” (BC). A perfect card counting system has BC = 1. I typically try to get values for the BC above 0.98 when I create card counting systems, though it is not always easy to do so. Systems with a BC below 0.98 arise due to the constraints of using a balanced count and having to make the system human feasible.
Here are the BC’s for System #1 and System #2 for a six-deck shoe:
- System #1 (1, -1, -1, 0, 0, 0, -1, -1, -1, 1) has BC = 0.925
- System #2 (2, -1, -1, -1, 0, 0, -1, -1, -1, 1) has BC = 0.972
The following table gives the results from using System #2 to card count the 19 Bet:
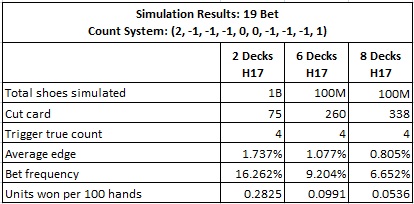
These simulations show a low vulnerability to card counting, no matter the number of decks used. The most vulnerable situation is two-decks, H17, where the card counter’s win-rate is 0.2825 units per 100 hands. This win-rate is approximately half that of ordinary blackjack card counting. Note that the win-rate for the six-deck case is 0.0991 units per 100 hands. Card counting a two-deck shoe yields about 3 times the win-rate of that available from counting a six-deck shoe.
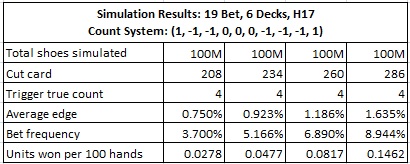
I now consider card counting the 19 Bet using System #1. The following table gives card counting results for various cut card placements:
Finally, I address the claims made in the documentation about the 19 Bet.
Claim 1: System #1 is “nearly optimal.”
As previously stated, the betting correlation for System #1 is 0.925 and for System #2 it is 0.972. To see what this means in practice, consider the case where the game is dealt from a six-deck shoe with the cut card placed one deck from the end (260 cards). As shown above, the win-rate is 0.0817 units per 100 hands using System #1. The previous table gives a win-rate of 0.0991 units per 100 hands using System #2. It follows that System #2 has a win-rate that yields 21.3% more profit than System #1. In other words, a minor change in the counting system resulted in a huge increase in performance. It is my opinion that System #1 is not “nearly optimal.”
Claim 2: The bet frequency is 9.283%
When dealt from a six-deck shoe, the bet frequency I obtained with the cut card placed 52 cards from the end is 6.89%. With the cut card placed at 26 cards, the bet frequency is 8.94%. I simulated 20M shoes with the cut card at 40 cards and obtained a bet frequency of 7.80%. No cut card placement gives a bet frequency close to 9.283%. I cannot reconcile the results I obtained with those presented in the documentation provided to me.
In the real world, the discrepancies outlined above have very little practical value. The conclusion of their mathematician was that the 19 Bet is safe from card counting. I agree with that conclusion. No reasonable AP is going to card count the 19 Bet.
I applaud the effort to include information on game protection in the developer’s documentation. All the correct steps were taken to have the work properly done and to present the results to prospective clients. However, as politicians are wont to say, “Mistakes were made.” Nevertheless, the folks behind Pick ‘Em Blackjack are ahead of the curve and deserve recognition for their good work.
I congratulate the developers of Pick ‘Em Blackjack for winning first place. I wish them much success.


