This post considers the blackjack side bet called "20 Pays" (20P). As the name implies, this wager wins whenever the player's first two cards total 20. In that sense, it is similar to both Royal 20s and Lucky Ladies. What makes this side bet unique is that it also pays if the player's first card is a Jack, Queen or King, when the second card is not ten-valued.
Here is the most common pay table for 20P:
- Jack of Diamonds pair with dealer BJ pays 1000-to-1
- Jack of Diamonds pair without dealer BJ pays 100-to-1
- Matched 20 (same rank and suit) pays 15-to-1
- Suited 20 (including A-9) pays 5-to-1
- Unsuited 20 (including A-9) pays 2-to-1
- First card J, Q or K (without a ten-valued second card) pays 1-to-1
- All others lose.
Here is the combinatorial analysis for 20P:
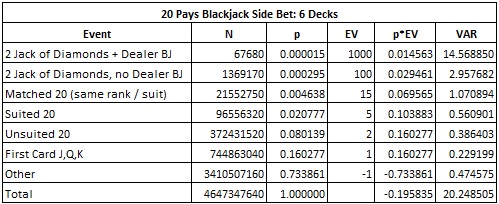
In particular,
- The house edge is 19.5835%.
- The hit frequency is 26.6139%
- The standard deviation is 4.4998
With a house edge over 19%, there is a lot to be done to overcome for card counting to become effective.
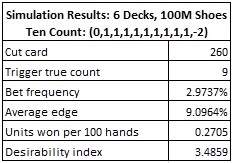
Intuitively, the Ten Count (0,1,1,1,1,1,1,1,1,-2) should be effective against 20P. The problem is in the way this count treats a Ten -- a Ten is both a good card and bad card. It is good in the sense that it creates more 20's. It is bad in the sense that it is not going to help getting the most common payout 1-to-1, which requires an abundance of Jacks, Queens and Kings.
A simulation of one hundred million (100,000,000) six-deck shoes shows a return of 0.2705 units per 100 hands when using the Ten Count. Here are the details of this simulation:
The following table gives the effect of removal for each card and a candidate counting system. Note, the EOR for a Jack is for a generic Jack, not the Jack of Diamonds:
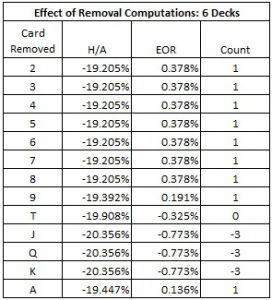
As shown in the table above, the other count system I analyzed has tags (1,1,1,1,1,1,1,1,1,0,-3,-3,-3), in other words,
- A, 2, 3, 4, 5, 6, 7, 8, 9 = +1
- T = 0
- J, Q, K = -3
Because of the value it assigns to a Ten, this count system has a relative weak betting correlation of 0.9630.
The following table gives the results from simulating one hundred million (100,000,000) six-deck shoes, using the count system above:
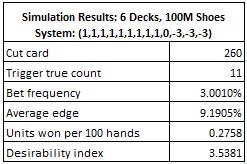
With a win rate of 0.2758 units per 100 hands, this system is just marginally stronger than the Ten Count (win rate of 0.2705 units per 100 hands). The 20P wager is on the low-end of vulnerability for blackjack side bets, no matter the count used against it.. With an eye towards simplicity, any AP who wants to target 20P by card counting will probably use the Ten Count.
I doubt any AP would seriously consider counting 20P by itself. However, if the AP is using the Ten Count to count insurance, then he may apply his count to 20P as well.
I did not consider the two-deck version, mainly because I don't have any evidence that 20P is available on a double-deck game.


