In the past few years there has been a proliferation of blackjack side bets based on the theme of the dealer busting. Among these side bets are “Bet the Bust,” “Bust Bonus,” “Bust It,” “Buster Blackjack,” and “Dealer Bust 21.” The market probably has room for one of these to be moderately successful: the winner of that battle is still to be determined. Among these, the wager “Bust It” (BI) has been around the longest. It is offered both as an ordinary blackjack side bet and as a side bet for Spanish 21. This article considers the countability of BI for ordinary blackjack. If a reader can confirm that they’ve recently seen BI available with Spanish 21, I will analyze that as well.
BI is a side bet that wins if the dealer busts with exactly 3 cards. If one or more players make a BI wager, then the dealer will draw a third card to any hand with a total of 12 to 16. This draw will take place even if there is no action left by any player at the table. The BI bet wins for the player if the dealer busts with exactly three cards. The payouts for winning BI bets are as follows:
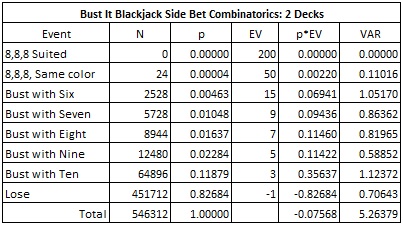
- Dealer busts with suited 8, 8, 8 pays 200-to-1.
- Dealer busts with colored 8, 8, 8 pays 50-to-1.
- Dealer busts with a six pays 15-to-1.
- Dealer busts with a seven pays 9-to-1.
- Dealer busts with an eight pays 7-to-1.
- Dealer busts with a nine pays 5-to-1.
- Dealer busts with a ten pays 3-to-1.
- Otherwise, the player loses the BI bet.
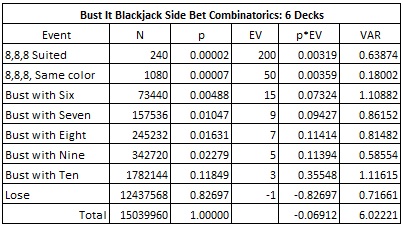
The following tables give the combinatorial analysis for the BI bet for 2 and 6 decks.
In particular, note that:
- The house edge for the two-deck version is 7.568%.
- The house edge for the six-deck version is 6.912%.
As usual, card counting is much stronger with two decks than with six decks. I will first consider the two-deck version.
The following table gives the effect of removal (EOR) for each card. The EOR tells the change in house edge by removing a single card of that rank and re-computing the house edge. A positive EOR means that the edge moves towards the player side if the card is removed. A negative EOR means that the edge moves towards the house side if the card is removed.
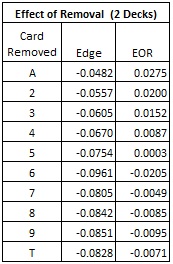
Note that by removing a single Ace from a two-deck game, the edge moves towards the player by 2.75%. This is a tremendous change in edge for a single card and indicates that this bet is highly countable. Intuitively, an Ace is the only card that cannot be part of a three-card busting hand, so removing Aces is very good for the player-side. Similarly, removing a single six from the two-deck game shifts the edge towards the house by 2.05%. A six forms the most bustable hand (T, 6). Likewise, sixes are required for the top payout of 15-to-1. The EOR for a seven is unexpectedly low. However, sevens create standing two-card totals (T, 7). Moreover, sevens only bust the two-card dealer starting totals of 15 and 16.
Based on these EOR’s, I developed and evaluated three card counting systems:
System #1 is the “optimal” system. I simply use the EOR’s to two decimal places, scaled to make the index for an Ace equal to 3. It is not feasible to use system #1 at the table, but it is useful to analyze as it gives an upper bound for the profit available by card counting BI.
- System #1 (optimal) = (3.00, 2.18, 1.65, 0.95, 0.03, -2.23, -0.53, -0.93, -1.03, -0.77).
System #2 is a balanced card counting system based on rounding the values given in system #1. The betting correlation for system #2 is 0.987, which means it captures 98.7% of the betting information available by using the optimal system #1.
- System #2 = (3, 2, 2, 1, 0, -2, 0, -1, -1, -1).
As a reminder of the notation I am using, the card counting tags are:
- A =+3
- 2, 3 = + 2
- 4 = +1
- 5, 7 = 0
- 6 = -2
- 8, 9, T = -1
System #2 is still too difficult for most APs to use in practice. It turns out there is an excellent alternative. System #3, given below, captures much of the strength of system #2 but can be learned in a few hours. The betting correlation for system #3 is 0.904, which means it captures 90.4% of the betting information available by using the optimal system #1.
- System #3 = (2, 1, 1, 0, 0, -2, 0, -1, -1, 0).
To analyze these three systems, I ran one hundred million (100,000,000) two-deck shoes, with the cut card placed at 75 cards, for each system. The following table summarizes the results of these simulations:
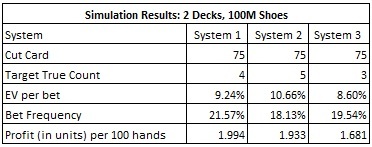
These numbers indicate a very high vulnerability to advantage play. If the AP uses system #2 on a fast heads-up double-deck game where he gets 200 rounds per hour, and the AP makes a $100 wager on BI whenever he has the edge, then the AP can earn $387 per hour. System #3 will return $336 per hour to this AP. The AP using system #2 will have an average edge over the house of 10.66% and will make the BI bet 18.13% of his hands.
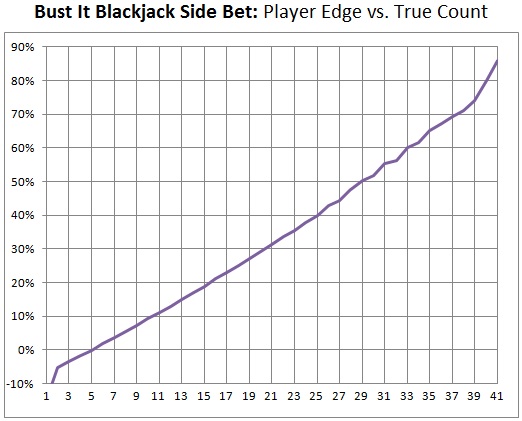
The following graph shows the player’s edge, using system #2, as a function of the true count. The player’s edge grows very fast compared to the ordinary blackjack card counter. For example, at a true count of +29, the AP will have an edge of about 50% over the house. The break-even true count is +5.
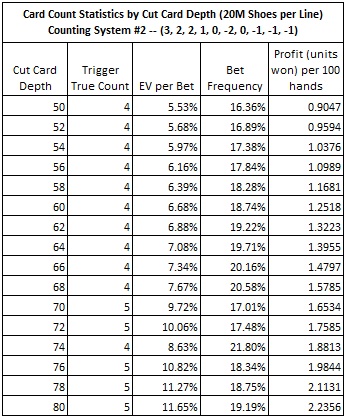
The most common approach to game protection is to reduce penetration between shuffles. The following table shows the card counting statistics for using system #2 against BI, for cut card depths from 50 cards to 80 cards. These results show that even with a shallow cut-card placement at 50 cards (less than one deck dealt between shuffles), BI still has a significant vulnerability to card counting.
The six-deck version of BI has the same pay table as the double-deck version. The house edge is slightly better for the player in the six-deck version, but the vulnerability of BI to card counting is significantly lower. The following table gives card counting statistics based on a simulation of twenty million (20,000,000) six-deck shoes. I assume the counter is using system #2 against the six-deck game and that the cut card is placed at 260 cards (one deck from the end):
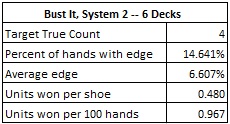
Against a six-deck shoe, the AP earns about half of what he can from the two-deck version. Playing the six-deck game with a deep cut at 52 cards (0.967 units per 100) is about the same as playing the two-deck version with a shallow cut of 52 cards (0.959 units per 100). In other words, a very good six-deck game is about the same as a mediocre two-deck game.
The following are my recommendations for protecting the BI side bet:
- Watch for players who place large wagers on the BI side bet several rounds into the shoe but don’t make a wager on the first hand.
- Watch out for team play, that is, a table full of players who are betting the BI bet together.
- Watch for the other usual tells that a card counting system is being used.
- Lessening the deck penetration between shuffles has minimal effectiveness, and may be cost-negative due to a reduced number of rounds per hour for legitimate play. I recommend against this remedy.
- Modify the pay table to make the house edge stronger.


